Алгебра, вопрос задал lianaspaskaya , 1 год назад

алгебра ..............

Приложения:

Ответы на вопрос

Ответил NNNLLL54

1

Ответ:

При вычислении определённого интеграла применяем формулу Ньютона-Лейбница .

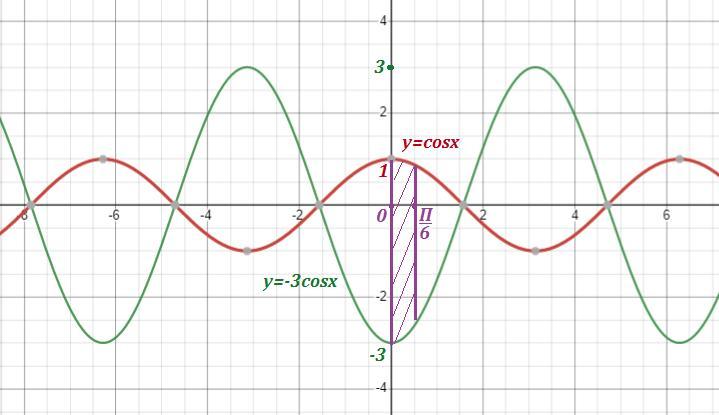
$\displaystyle \bf 1)\ \ \int\limits^1_{-1}\, (x+1)^3\, dx=\frac{(x+1)^4}{4}\, \Big|_{-1}^1=\frac{(1+1)^4}{4}-\frac{(-1+1)^4}{4}=\frac{2^4}{4}-0=4\\\\\\\int\limits^{2\pi }_{\pi }\, sin\frac{x}{2}\, dx=-2\, cos\frac{x}{2}\, \Big|_{\pi }^{2\pi }=-2\, cos\pi +2\, cos\frac{\pi }{2}=-2\cdot (-1)+2\cdot 0=2$

2) Найти площадь фигуры, ограниченной линиями

$\bf y=cosx\ \ ,\ \ y=-3cosx\ ,\ \ x=0\ \ ,\ \ x=\dfrac{\pi }{6}$ .

Площадь области равна

$\displaystyle \bf S=\int\limits^{\pi /6}_{0}\, (\, cosx-(-3cosx)\, )\, dx=\int\limits^{\pi /6}_{0}\, 4\, cosx\, dx=4\, sinx\, \Big|_0^{\pi /6}=\\\\\\=4\cdot \Big(sin\frac{\pi }{6}-sin\, 0\Big)=4\cdot \Big(\frac{1}{2}-0\Big)=2$

На рисунке область заштрихована .

Приложения:

lianaspaskaya: Большое спасибо, в профиле ещё задание по алгебре, помогите пожалуйста

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Литература, 1 год назад

міні твір на тему Література мені потрібна для того щоб... 3-5 речень строчноооооо...

Математика, 1 год назад

В начальных классах одной городской школы обучаются 260 учеников в средних-340,остольные-в старших. Сколько учеников в старших классах,если всего в ней обучаются 980 учащихся?

Химия, 1 год назад

Що спільного і в чому відмінність між молярною масою і відносною молекулярною масою? Дуже срочно!

Химия, 1 год назад

Наведіть по п'ять прикладів основних та кислотних оксидів та дайте їм назви.

Қазақ тiлi, 6 лет назад

5-тапсырма. Төмендегі тірек сөздерді қолдана отырып, көсемшені қатыстырып сөйлемдер құраңдар. Жіктік жалғауын дұрыс қойыңдар. Үлгі: Мектеп қабырғасы, музыка, құру, ансамблін, Бақытжан Байқадамов,...

Литература, 6 лет назад

Напишите цитаты Катерины (Островский, "Гроза"), свидетельствующие о её постоянной борьбе...