Алгебра, вопрос задал Dhejejjdj , 6 лет назад

Алгебра 10 класс, доказать тождество, помогите пожалуйста

Приложения:

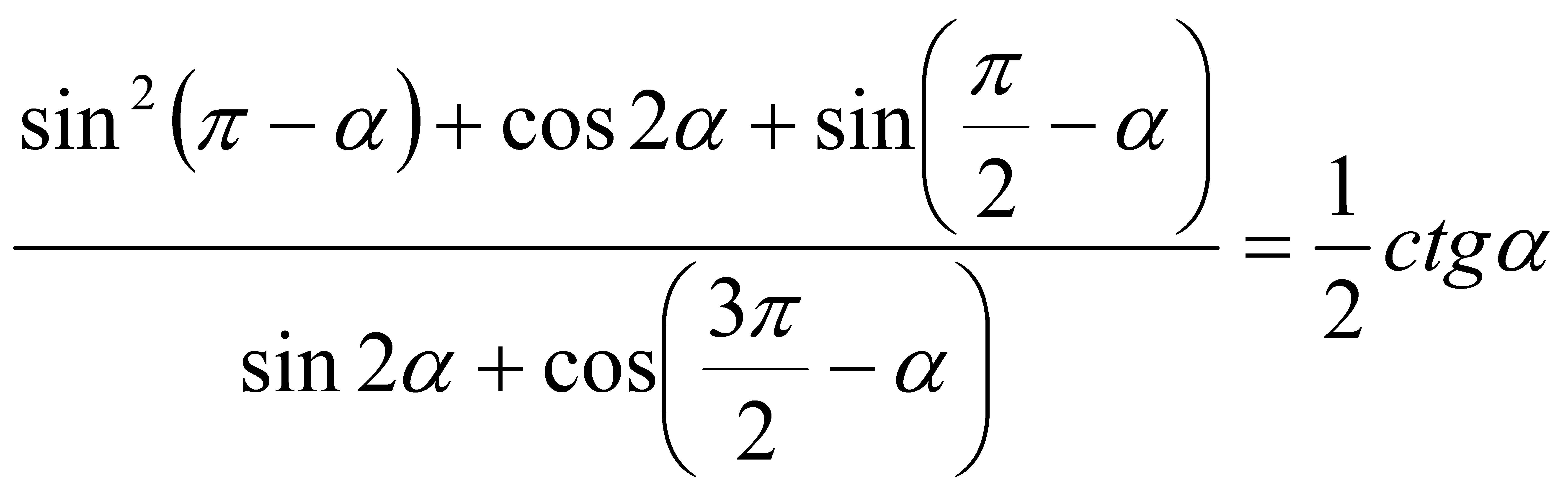
Vopoxov: Точно без ошибки? у меня не сходится

someman234: но тут же ошибка, не получается

Ответы на вопрос

Ответил Vopoxov

Объяснение:

$\frac{\sin ^{2} (\pi {- }\alpha ) + \cos 2\alpha + \sin( \frac{\pi}{2}{ - }\alpha ) }{ \sin2 \alpha + \cos(\frac{3\pi}{2} - \alpha ) } = \frac{1}{2} \ctg \alpha \\$

Преобразуем левую часть:

$\frac{\sin ^{2} (\pi {- }\alpha ) + \cos 2\alpha + \sin( \frac{\pi}{2}{ - }\alpha ) }{ \sin2 \alpha + \cos(\frac{3\pi}{2} - \alpha ) } = \\ = \frac{\sin ^{2} \alpha + ( \cos^{2} \alpha - \sin^{2} \alpha ) + \cos\alpha }{ 2\sin \alpha \cos \alpha - \sin \alpha } = \\ = \frac{\cancel{\sin ^{2} \alpha \: } + ( \cos^{2} \alpha - \cancel{\sin^{2} \alpha }) + \cos\alpha }{ \sin \alpha (\cos \alpha - 1) } = \\ = \frac{ \cos^{2} \alpha + \cos\alpha }{ \sin \alpha (2\cos \alpha - 1) } = \frac{ \cos \alpha (\cos\alpha+1) }{ \sin \alpha (2\cos \alpha - 1) }= \\=\frac{\cos\alpha+1 }{ 2\cos \alpha - 1 } \cdot\frac{ \cos \alpha}{ \sin \alpha} = \frac{\cos\alpha+1 }{ 2\cos \alpha - 1 }\cdot\ctg \alpha =\\ = \frac{(\cos\alpha-0,5)+1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \frac{(\cos\alpha-0,5) }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha+\frac{1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \frac{1 }{ 2}\cdot\ctg \alpha+\frac{1,5 }{ 2(\cos \alpha - 0,5)}\cdot\ctg \alpha=\\= \bigg( \frac{1 }{ 2}\cdot\ctg \alpha\bigg)+\frac{3 }{ 4\cos \alpha - 2)}\cdot\ctg \alpha$

Это максимум. Левая и правая части, очевидно, не совпадают (в скобках выделено выражение совпадающее с правой частью, но сдева также есть дополнительные члены, отсутствующие справа)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

здравствуйте, помогите пожалуйста составить план по русскому языку на тему почему праздник 9 мая священный для нас.

Математика, 1 год назад

на ферме 120 коров и 121 телёнок для них заготовили силос из расчёса 5636 кг на одну корову и 2485 на одного телёнка сколько всего силоса заготовили для животных ОБЬЯСНЕНИЕ...

Математика, 6 лет назад

Знайти площу фігури, обмеженої лініями y=3/x, y=2x+1, x=3.

Математика, 6 лет назад

осьовий переріз циліндра квадрат площа якого 8 см квадрат знайдіть площу основи циліндра...

Алгебра, 8 лет назад

Квадрат задуманного числа на 14 меньше чем произведение двух чисел больших задуманного на 1 и на 2 соответственно (Найдите задуманное число)...

Биология, 8 лет назад

как найти сколько у человека хромосом.помогите пжжжж.биология 6 класс...