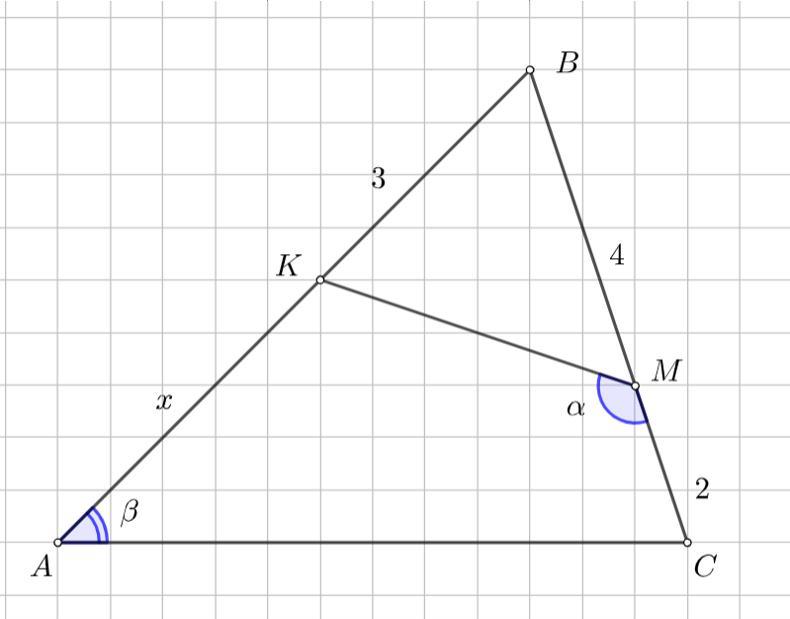
Альфа + бета = 180°. По данным рисунка найдите AK

Дано:

α + β = 180°;

BК = 3; ВМ = 4; МС = 2.

Найти:

АК- ?

                                              Решение

Так как α + β = 180° (по условию), то α = 180 - β.

∠КМВ — смежный с углом α, а так как сумма смежных углов равна 180°, то ∠КМВ = 180 - α = 180 - (180 - β)  = 180 - 180 + β = β.

Значит, ∠BAC = ∠BMK.

∠КВМ — общий угол для треугольников MBK и АВС.

Тогда Δ MBK ~ Δ АВС по первому признаку (по двум углам).

У подобных треугольников сходственные стороны пропорциональны.

Стороне BК треугольника MBK соответствует сторона ВС треугольника АВС, так как эти стороны лежат напротив равных углов. Аналогично, стороне ВМ треугольника MBK соответствует сторона АВ треугольника АВС.

Запишем пропорцию:

BM = 4 и ВК = 3, по условию.

АВ = AK + BК = х + 3;

ВС = ВМ + МС = 4 + 2 = 6.

Подставляем длины сторон в пропорцию:

Произведение крайних членов пропорции равно произведению средних членов, поэтому можем записать такое уравнение:

3(х + 3) = 4 ∙ 6 ;

3х + 9 = 24;

3х = 24 - 9;

3х = 15;

х = 15 : 3;

х = 5.

Ответ: АК = 5.