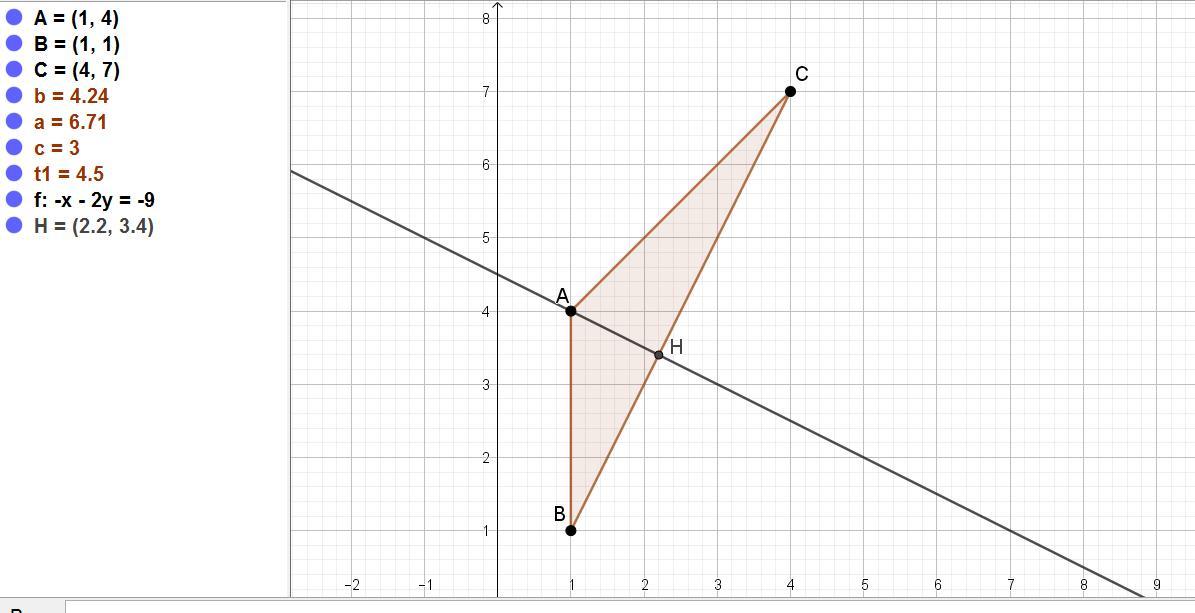
AH - высота треугольника ABC. Зная координаты точек A(1;4), B(1;1) , C(4;7) найти координаты точки H.
Ответ (2;3), нужно решение
Ответы на вопрос
Даны координаты точек A(1;4), B(1;1) , C(4;7).
Уравнение прямой, включающей сторону ВС:
Вектор BC : (4-1=3; 7-1=6) = (3; 6).
(x - 1)/3 = (у - 1)/6, после сокращения знаменателей на 2, получаем:
(x - 1)/1 = (у - 1)/2 это каноническое уравнение стороны ВС.
Или 2х - 2 = у - 1 или 2х - у - 1 = 0 общее уравнение.
у = 2х - 1 с угловым коэффициентом. к(ВС) = 2.
Угловой коэффициент перпендикуляра АН к стороне ВС равен:
к(АН) = -1/к(ВС) = -1/2.
Уравнение АН: у = (-1/2)х + в. Для определения параметра в подставим координаты точки А: 4 = (-1/2)*1 + в, отсюда в = 4 + (1/2) = 9/2.
Уравнение АН: у = (-1/2)х + (9/2).
Координаты точки Н находим как точки пересечения прямых АН и ВС.
(-1/2)х + (9/2) = 2х - 1,
(5/2)х = (11/2), отсюда находим х(Н) = 11/5 = 2,2.
у(Н) = 2*(11/5)-1 = 17/5 = 3,4.
Ответ: Н(2,2; 3,4).