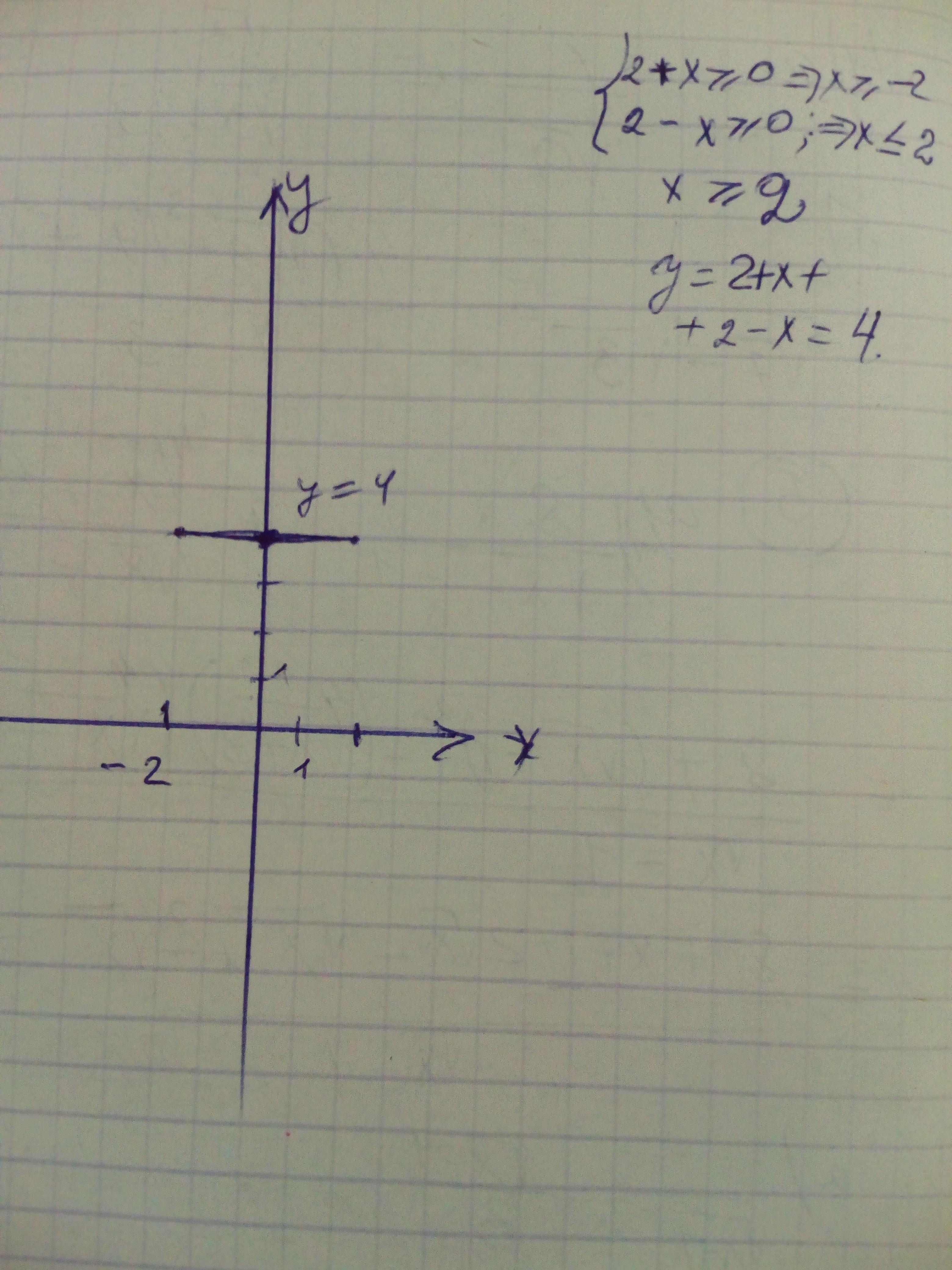Агебра 10 класс.(15 баллов )
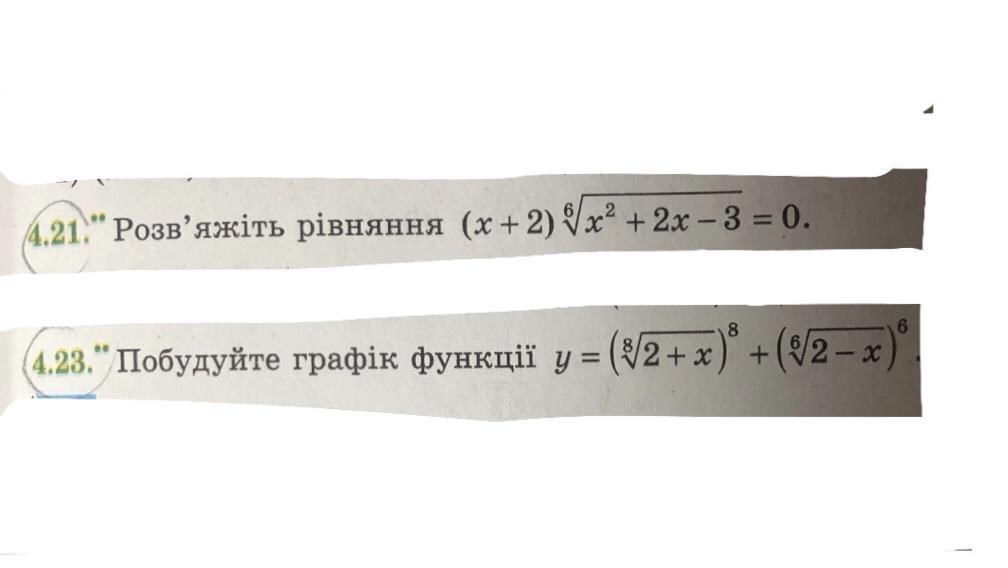
Ответы на вопрос
№21
ОДЗ х²+2х-3≥0; х²+2х-3=0; найдем корни кв. трехчлена по т. обратной т. Виета: х1*х2=-3; х1+х2=-2; х1=-3; х2=1
-------------------[-3]---------[1]----------->x
+ - +
ОДЗ х∈(-∞; -3]U[1; ∞)
х+2=0; х=-2 ∉ОДЗ
⁶√(х²+2х-3)=0 при х1=-3; х2=1.
Ответ: -3; 1.
№23
у=(⁸√(2+х))⁸+ (⁶√(2-х))⁶; 2+x≥0; x≥-2; 2-x≥0; x≤2
D(y)=[-2; 2]
На этом интервале подкоренные выражения ≥0
у=2+х+2-х=4
График - отрезок прямой ║ оси ОХ и проходящий через точку (0; 4) от точки (-2;4) до точки (2;4).
^у
I
I(0; 4)
---------I--------- у=4
-----[-2]------I-------[2]----------------------------------------------------->x
I
1. Произведение равно нулю, когда хотя бы один из сомножителей равен нулю. Поэтому х=-2, но надо посмотреть, существует ли корень при этом значении, разложим на линейные множители подкоренное выражение. х²+2х+3=0, по теореме, обратной теореме Виета, корнями этого уравнения будут -3 и 1, разобьем этими числами числовую ось и найдем область определения корня четной степени. х²+2х+3≥0, неравенство решим методом интервалов. (х+3)(х-1)≥0
________-3______________1__________
+ - +
Как видим, найденный корень х=-2 не попал в область определения. Значит, из области определения (-∞-3]∪[1;+∞) подходят только корни -3 и 1
2.График построю во вложении. Это отрезок прямой у=4, на отрезке х∈[-2;2]