Ae и DE сегменты ABCD параллелограмм биссектрисы и E - BS
стена, а стена F - AD соответствует соответствующим точкам. Известно, что EF ⊥ AD. Если AB = 5 см,
Если EF = 2 см, найдите:
а) стена АД параллелограмма;
б) площадь параллелограмма ABCD
Ответы на вопрос
Ответил siestarjoki
0
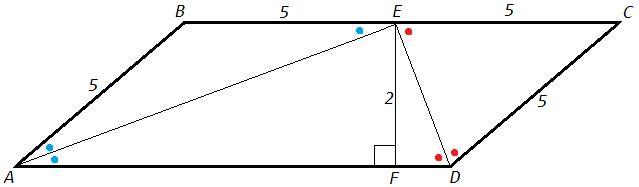
AE и DE - биссектрисы параллелограмма ABCD, точка E лежит на BC. Точка F лежит на AD, EF⊥AD. AB=5 см, EF=2 см.
Найти a) AD; б) S(ABCD).
-------------------------------------------------------------------
∠BAE=∠DAE (AE - биссектриса)
∠DAE=∠BEA (накрест лежащие при BC||AD)
∠BAE=∠BEA => △ABE - равнобедренный, AB=BE
Аналогично EC=CD
AB=CD=5 см, AD=BC (противоположные стороны параллелограмма)
a) AD =BC =BE+EC =AB+CD =5+5=10 (см)
б) S(ABCD) =AD*EF =10*2 =20 (см^2) (EF - высота)
Приложения:
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Геометрия,
7 лет назад
Математика,
8 лет назад
Математика,
8 лет назад