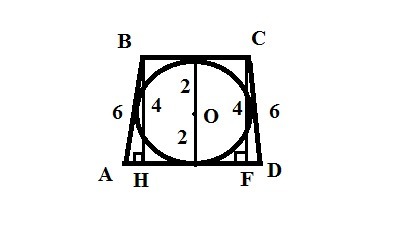
abcd равнобедренная трапеция bc параллельно ad ab=cd=6 В трапецию вписана окружность радиусом 2 найдите основание трапеции

Проведём высоту ВК⊥АД. Диаметр окружности, вписанной в трапецию, равен высоте трапеции. ВК=2R=4.

В треугольнике АВК АК=√(АВ²-ВК²)=√(6²-4²)=√20=2√5.

В равнобедренной трапеции ВС=АД-2АК=АД-4√5.

Суммы противолежащих сторон описанной трапеции равны, значит АД+ВС=АВ+СД=6+6=12.

АД+АД-4√5=12,
2АД=12+4√5,
АД=2(3+√5)  - это ответ.

Высота трапеции BH=2*2=4.
По теореме Пифагора
AH=√AB²-BH²=√6²-4²=√36-16=√20=√4·5=2√5
FD=AH=2√5
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
AB+CD=AD+BC
AD+BC=12
AD=AH+HF+FD=2√5+BC+2√5=BC+4√5
2BC+4√5=12
BC=6-2√5
AD=6+2√5