А7 и В1 помогите пожалуйста! Срочно!!!

А7. Треугольник ABC - прямоугольный, угол В=90 гр.
Значит, по т.Пифагора: 


По определению синуса: 

По определению косинуса: 

По определению тангенса: 

Ответ: вариант 3)

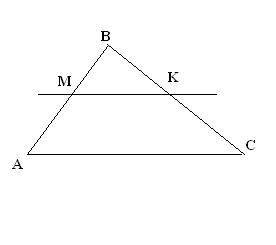
В1. Рисунок прикреплен.
1) Рассмотрим треугольники ABC и BMK. Они подобны по 2 признаку подобия (2 равных угла):
угол В - общий
угол BMK = угол BAC - как соответственные углы при MK || AC и секущей AB
Т.к. треугольники подобны, то:
(*)

Такое значение отношения следует из того, что по условию , а это значит, что сторона AB составляет 5 частей. Тогда 

Из (*) следует, что:




2) Запишем периметры треугольников:

см.

Ответ: 5 см.