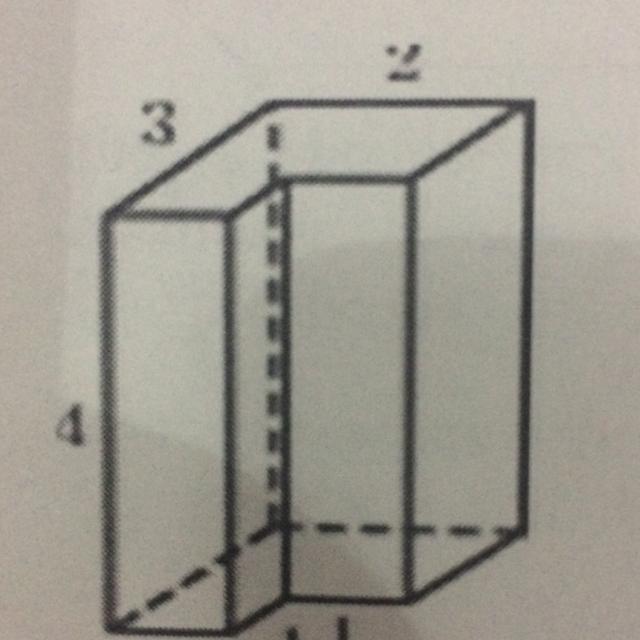
А5. Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).
Помогите пожалуйста
Спасибо вам большое!
Ответы на вопрос
Ответ:
50
Объяснение:
1) Так как все двугранные углы данного многогранника прямые, то он является прямой призмой, и все его боковые грани являются прямоугольниками.
Площадь поверхности S прямой призмы равна сумме площадей её оснований S осн и боковой поверхности S бок:
S = S осн + S бок
2) Так как все углы верхнего основания прямые, то его площадь равна разности площадей прямоугольника с размерами 3 х 2 (3 в длину, 2 в ширину) и углового выреза с размерами 1 х 1 (1 в длину, 1 в ширину):
3 · 2 - 1 · 1 = 6 - 1 = 5
А так как нижнее основание в прямой призме равно верхнему основанию, то площадь нижнего основания также равна 5, а площадь двух оснований равна:
S осн = 5 · 2 = 10
3) Площадь боковой поверхности прямой призмы S бок равна произведению периметра её основания P на высоту Н, которая в прямой призме равна длине бокового ребра (согласно рисунку, боковое ребро равно 4, следовательно, высота Н =4):
S бок = Р · H
Р = 3 + 2 + (3-1) + 1 + 1 + (2-1) = 10
S бок = Р · H = 10 · 4 = 40
4) Площадь поверхности многогранника, изображенного на
рисунке:
S = S осн + S бок = 10 + 40 = 50
Ответ: площадь поверхности многогранника, изображенного на
рисунке, равна 50.