Алгебра, вопрос задал Аноним , 1 год назад

А10 Решение тригонометрических уравнений

Приложения:

Ответы на вопрос

Ответил Аноним
1

\sin\left(3x+\dfrac{\pi}{3}\right)=0\\ \\ 3x+\dfrac{\pi}{3}=\pi k,k \in \mathbb{Z}\\ \\ 3x=-\dfrac{\pi}{3}+\pi k,k \in \mathbb{Z}\\ \\ x=-\dfrac{\pi}{9}+\dfrac{\pi k}{3}, k \in \mathbb{Z}

Корни, лежащие на промежутке [0;π].

k=1;~~~ x=-\dfrac{\pi}{9}+\dfrac{\pi}{3}=-\dfrac{\pi}{9}+\dfrac{3\pi}{9}=\dfrac{2\pi}{9}\\ \\ k=2;~~ x=-\dfrac{\pi}{9}+\dfrac{2\pi}{3}=-\dfrac{\pi}{9}+\dfrac{6\pi}{9}=\dfrac{5\pi}{9}\\ \\ k=3;~~~ x=-\dfrac{\pi}{9}+\pi=-\dfrac{\pi}{9}+\dfrac{9\pi}{9}=\dfrac{8\pi}{9}

Ответил PVJ
1

Відповідь:

Пояснення:

Приложения:
Предыдущий вопрос
Следующий вопрос
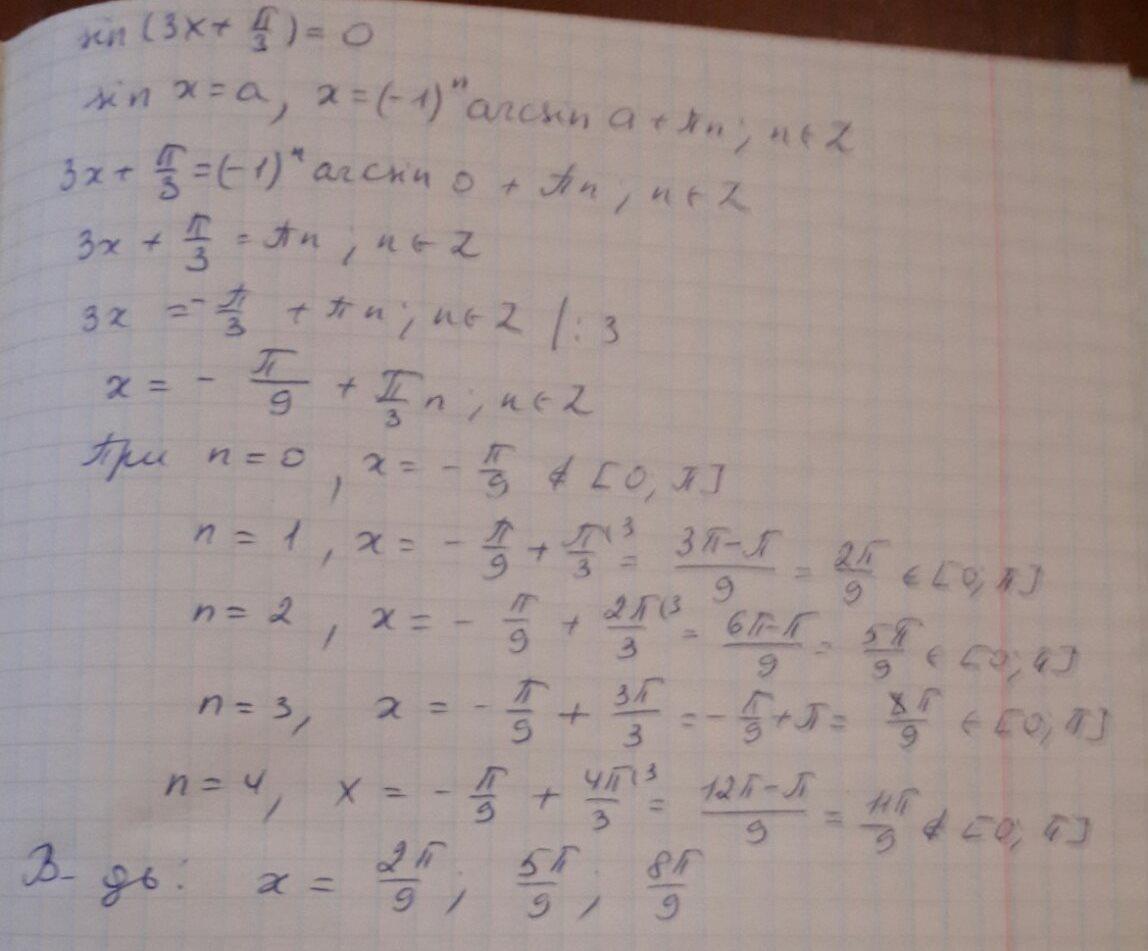
Новые вопросы