Алгебра, вопрос задал Аноним , 6 лет назад

((a + 2)/Sqrt[2 a] - a/(Sqrt[2 a] + 2) + 2/(a - Sqrt[2 a])) ((Sqrt[a] - Sqrt[2])/(a + 2))

Приложения:

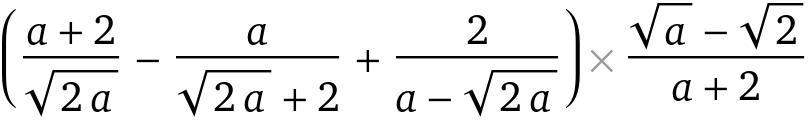
Ответы на вопрос

Ответил MatemaT123

Ответ:

$\dfrac{a+4}{(\sqrt{a}+\sqrt{2})(a+2)}$

Объяснение:

$1) \ \dfrac{a+2}{\sqrt{2a}}-\dfrac{a}{\sqrt{2a}+2}=\dfrac{(a+2)(\sqrt{2a}+2)-a\sqrt{2a}}{\sqrt{2a}(\sqrt{2a}+2)}=\dfrac{a\sqrt{2a}+2a+2\sqrt{2a}+4-a\sqrt{2a}}{\sqrt{2a}(\sqrt{2a}+2)}=$

$=\dfrac{2a+2\sqrt{2a}+4}{\sqrt{2a}(\sqrt{2a}+2)};$

$2) \ \dfrac{2a+2\sqrt{2a}+4}{\sqrt{2a}(\sqrt{2a}+2)}+\dfrac{2}{a-\sqrt{2a}}=\dfrac{(2a+2\sqrt{2a}+4)(a-\sqrt{2a})+2\sqrt{2a}(\sqrt{2a}+2)}{\sqrt{2a}(\sqrt{2a}+2)(a-\sqrt{2a})}=$

$=\dfrac{2a^{2}-2a\sqrt{2a}+2a\sqrt{2a}+2(\sqrt{2a})^{2}-4\sqrt{2a}+2(\sqrt{2a})^{2}+4\sqrt{2a}}{((\sqrt{2a})^{2}+2\sqrt{2a})(a-\sqrt{2a})}=$

$=\dfrac{2a^{2}+2 \cdot 2a+2 \cdot 2a}{(2a+2\sqrt{2a})(a-\sqrt{2a})}=\dfrac{2a^{2}+4a+4a}{2(a+\sqrt{2a})(a-\sqrt{2a})}=\dfrac{2a^{2}+8a}{2(a^{2}-(\sqrt{2a})^{2})}=$

$=\dfrac{2(a^{2}+4a)}{2(a^{2}-2a)}=\dfrac{a^{2}+4a}{a^{2}-2a};$

$3) \ \dfrac{a^{2}+4a}{a^{2}-2a} \cdot \dfrac{\sqrt{a}-\sqrt{2}}{a+2}=\dfrac{a(a+4)(\sqrt{a}-\sqrt{2})}{a(a-2)(a+2)}=\dfrac{(a+4)(\sqrt{a}-\sqrt{2})}{(\sqrt{a}-\sqrt{2})(\sqrt{a}+\sqrt{2})(a+2)}=$