9. У результаті перетину двох прямих один з утворених кутів у 7 разів менший від суми
трьох інших. Знайди найменший кут, утворений при перетинi прямих.
45°
35°
25°
15°

Ответ:

Найменший кут, утворений при перетині двох прямих дорівнює 45°.

Объяснение:

У результаті перетину двох прямих один з утворених кутів у 7 разів менший від сумитрьох інших. Знайди найменший кут, утворений при перетинi прямих.

При перетині двох прямих утворюються дві пари вертикальних та чотири пари суміжних кутів.

• Два кути, у яких одна сторона спільна, а дві інші сторони є доповняльними променями, називаються суміжними.

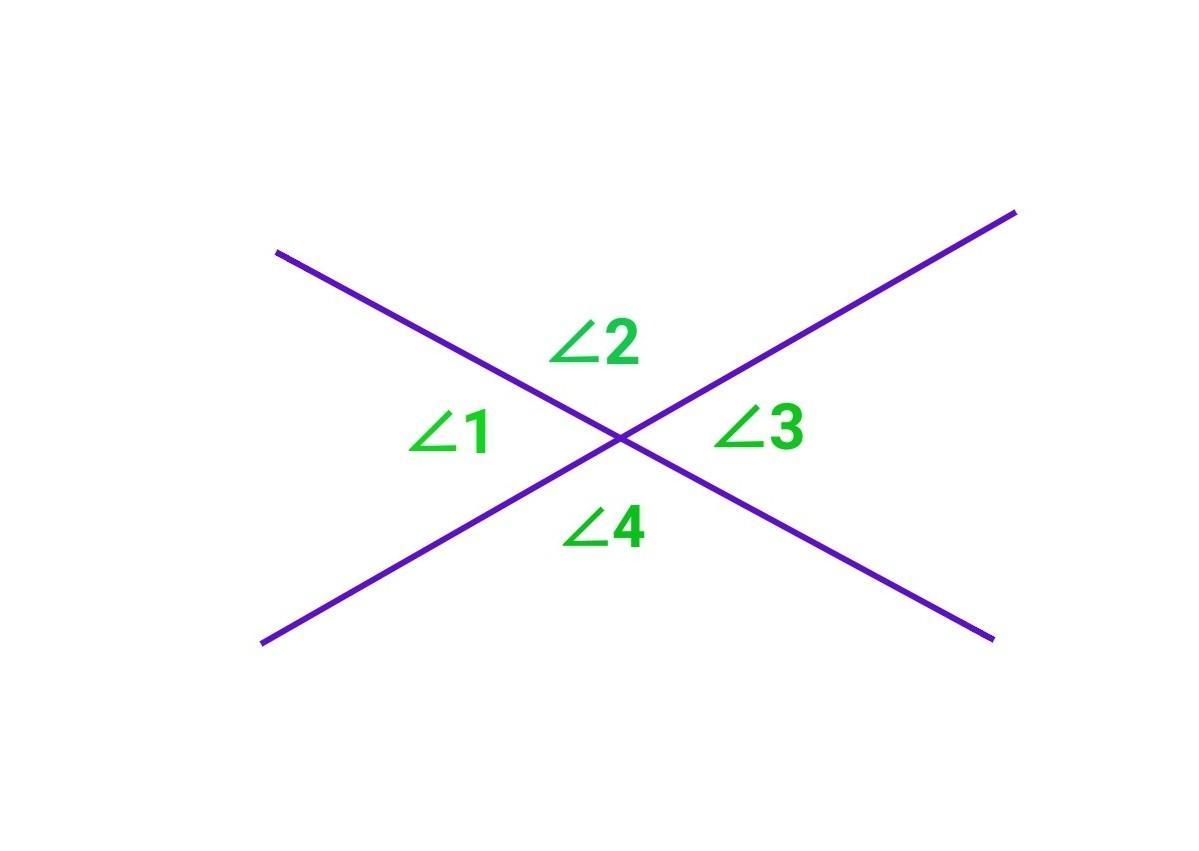
∠1 і ∠2, ∠2 і ∠3, ∠3 і ∠4, ∠1 і ∠4- суміжні

• Сума суміжних кутів дорівнює 180°
• Два кути називаються вертикальними, якщо обидві сторони одного кута є продовженням сторін другого.

∠1 та ∠3, ∠2 та ∠4 - вертікальні.

Розв'язання

Нехай ∠1 = ∠3 = х - як вертикальні, тоді ∠2 = ∠4 = (180°-х) - як суміжні з кутами ∠1 і ∠3.

З умовою:

∠2 + ∠3 + ∠4 = 7 • ∠1.

Розв'яжемо рівняння:

180° -х + х + 180° - х = 7х

8х = 360°

х = 360° : 8

х = 45°

Отже, ∠1 = ∠3 = 45°, ∠2 = ∠4 = 180° - 45° = 135°.

Найменший кут, утворений при перетині прямих дорівнює 45°.

#SPJ1