Математика, вопрос задал Jacksoon95 , 7 лет назад

82 Б. Здравствуйте, помогите решать уравнение. Не срочно . Найти общий интеграл уравнения в полных дифференциалах

Приложения:

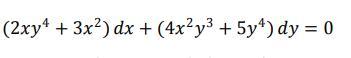
Ответы на вопрос

Ответил Correlation

0

В уравнении $M(x;y)=2xy^4+3x^2;~~ N(x;y)=4x^3y^3+5y^4$ . Действительно, $dfrac{partial M}{partial y}=8xy^3=dfrac{partial N}{partial x}$ , т.е. дифференциальное уравнение является уравнением в полных дифференциалах.

Интегрируя по х

$F(x;y)=displaystyle int M(x;y)dx=int(2xy^4+3x^2)dx=x^2y^4+x^3+C(y)$

Теперь эту функцию продифференцируем по у.

$F'_y(x;y)=4x^2y^3+C'(y)$

Видим, что $F'_y(x;y)=N(x;y)=5y^4+4x^3y^3$ отсюда $C'(y)=5y^4$ , получим $C(y)=displaystyle int 5y^4 dy=y^5$

Общий интеграл: $y^5+x^2y^4+x^3=C$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Помогите пожалуйста!!! Put the verbs in brackets into the correct tense form.Между словами ставим один пробел. Записываем/вводим только необходимую форму глагола возле соответствуещего номера!

Русский язык, 1 год назад

Из предложений исчезли одлежащие. Догадайся, что это за слова, и выпиши их. __________ - это сказочный персонаж, который умеет совершать чудеса. Если наклеить на лист кусочки цветной бумаги,...

Биология, 7 лет назад

1- Совокупность организмов одного вида, длительное время обитающих на одной территории (занимающих определённый ареал) и частично или полностью изолированных от особей других таких же групп,...

ОБЖ, 7 лет назад

помоги пожалуйста пожалуйста...

Литература, 8 лет назад

в творчестве ШЕКСПИРА,гете,СКОТТА пушкина привлекало,-пишет литературовед Л.фризман,- умение передать историческую действительность...

Математика, 8 лет назад

7^(x-3) + 7^(x-2) + 2 * 7^(x-1) = 106...