76 задание, с решением
Приложения:
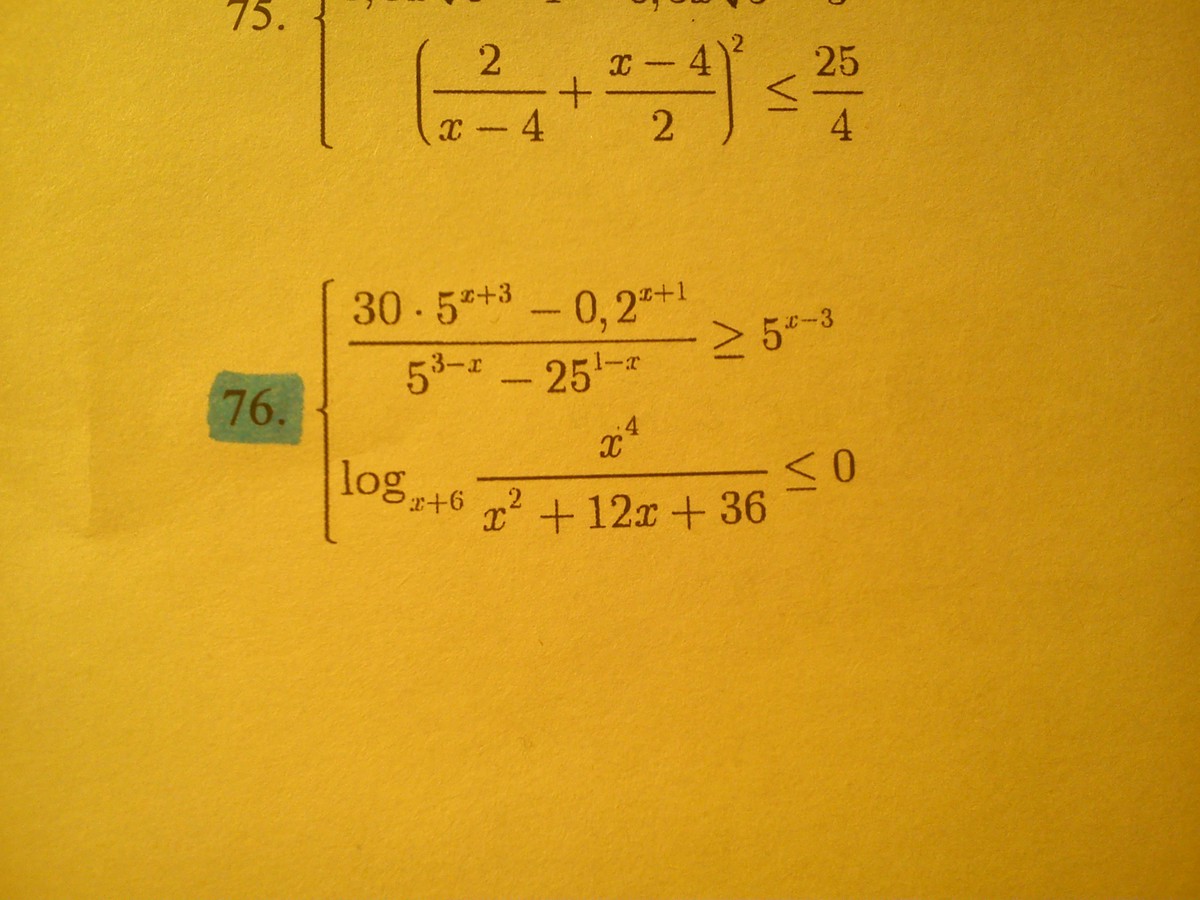
Ответы на вопрос
Ответил oganesbagoyan
0
собирая все члены первого неравенства в левую часть и делая несложные преобразование получаем
125*30*5^x / 25*5 ^(-x)*(5 -5^(-x))≥0 ⇒ 5 - 5^(-x) > 0 ⇒5 > 5^(-x) ⇒ x > -1x +6> 5
===============================================================
(125*30*5^x -1) / 25*5 ^(-2x)*(5^x - 1)) ≥0 ⇒ (125*30*5^x -1) / (5^x - 1)) ≥0
(x+6) > 0 ⇒ Loq _(x+6) (x^4/(x+6)² =2*Loq _(x+6) (x²/(x+6)) = 2(Loq _(x+6) x² -1) .
Loq_(x+6) x² ≤ 1.
x+6 >4 >1 ⇒ 0 ≤x² ≤ x+6⇔ x² -x -6 ≤0 ⇔(x+2)(x-3)≤ 0 ⇒ -2≤x≤3 учитывая из решения первого неравенства системы окончательно получается
ответ : -1<x ≤-3 или иначе x∈ (-1;3 ] .
125*30*5^x / 25*5 ^(-x)*(5 -5^(-x))≥0 ⇒ 5 - 5^(-x) > 0 ⇒5 > 5^(-x) ⇒ x > -1x +6> 5
===============================================================
(125*30*5^x -1) / 25*5 ^(-2x)*(5^x - 1)) ≥0 ⇒ (125*30*5^x -1) / (5^x - 1)) ≥0
(x+6) > 0 ⇒ Loq _(x+6) (x^4/(x+6)² =2*Loq _(x+6) (x²/(x+6)) = 2(Loq _(x+6) x² -1) .
Loq_(x+6) x² ≤ 1.
x+6 >4 >1 ⇒ 0 ≤x² ≤ x+6⇔ x² -x -6 ≤0 ⇔(x+2)(x-3)≤ 0 ⇒ -2≤x≤3 учитывая из решения первого неравенства системы окончательно получается
ответ : -1<x ≤-3 или иначе x∈ (-1;3 ] .
oganesbagoyan:
надо корректировать
Новые вопросы
Английский язык,
1 год назад
Беларуская мова,
1 год назад
Русский язык,
1 год назад
История,
7 лет назад