70 БАЛЛОВ !
Пожалуйста, помогите решить математику, выходит 2 за полугодие :с
Приложения:
Ответы на вопрос
Ответил Regent1828
0
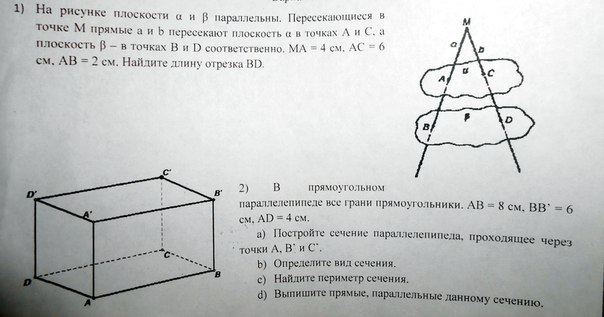
1) По сути дела, задача сводится к доказательству подобия треугольников
МАС и МВD. (Смотри файл).
Так как плоскости α и β параллельны, то прямые, проходящие через отрезки АС и ВD также параллельны. По теореме Фалеса параллельные прямые откладывают на сторонах угла взаимно пропорциональные отрезки.
Тогда ΔМАС подобен ΔМВD по двум сторонам и общему углу с коэффициентом подобия k = МВ/МА = 1,5. Следовательно, третьи стороны этих треугольников АС и ВD подобны с тем же коэффициентом.
Так как АС = 6 см, то ВD = k*АС = 9 см
Ответ: 9 см
2) a) Сечение наложенное диагональное.
b) Так как АВ=8 см а ВВ¹=6 см, то АВ¹ = √64+36 = 10 см
АD = 4 см. Тогда периметр сечения АDC¹B¹: P = 2*(4+10) = 28 см
c) Прямые, параллельные данному сечению: A¹D¹; CB, а также прямые,
входящие в плоскость сечения: AD; C¹B¹
МАС и МВD. (Смотри файл).
Так как плоскости α и β параллельны, то прямые, проходящие через отрезки АС и ВD также параллельны. По теореме Фалеса параллельные прямые откладывают на сторонах угла взаимно пропорциональные отрезки.
Тогда ΔМАС подобен ΔМВD по двум сторонам и общему углу с коэффициентом подобия k = МВ/МА = 1,5. Следовательно, третьи стороны этих треугольников АС и ВD подобны с тем же коэффициентом.
Так как АС = 6 см, то ВD = k*АС = 9 см
Ответ: 9 см
2) a) Сечение наложенное диагональное.
b) Так как АВ=8 см а ВВ¹=6 см, то АВ¹ = √64+36 = 10 см
АD = 4 см. Тогда периметр сечения АDC¹B¹: P = 2*(4+10) = 28 см
c) Прямые, параллельные данному сечению: A¹D¹; CB, а также прямые,
входящие в плоскость сечения: AD; C¹B¹
Приложения:
Новые вопросы