Алгебра, вопрос задал udalena70 , 1 год назад

70 баллов ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА

Приложения:

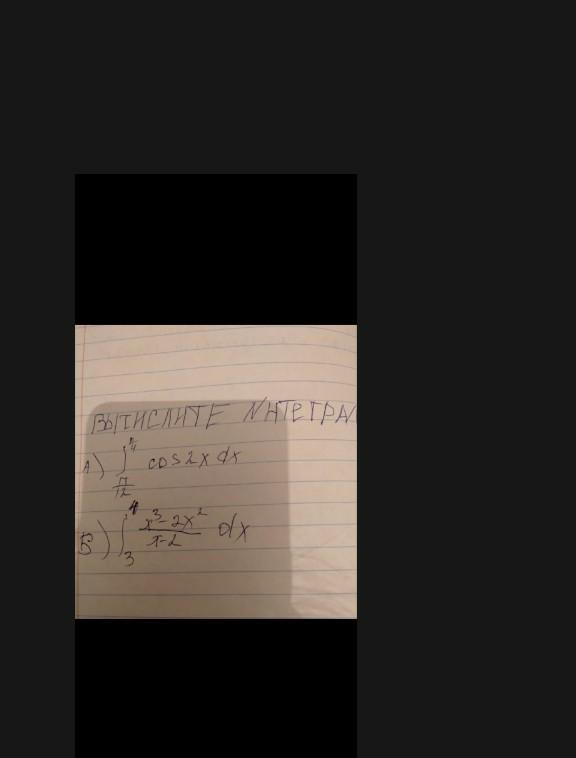
Ответы на вопрос

Ответил Fire1ce

Ответ:

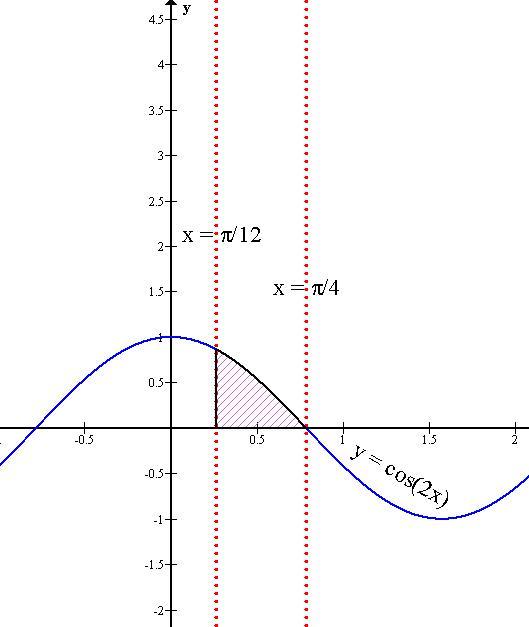
1) Значение определённого интеграла функции y=cos(2x) от π/12 до π/4 равно 0.25.

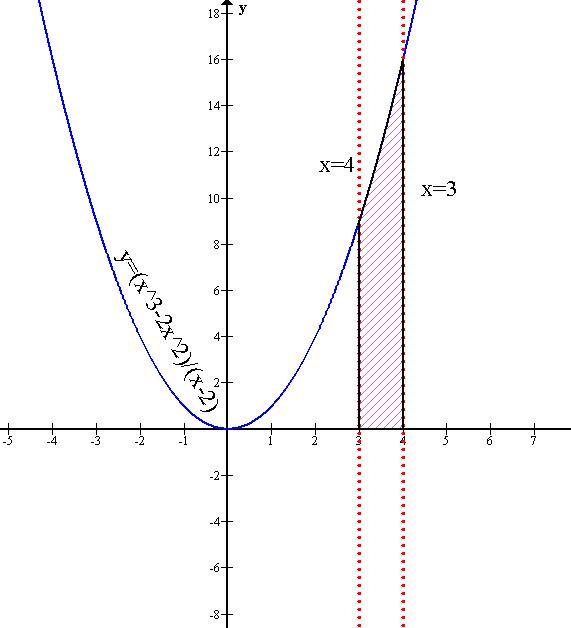
2) Значение определённого интеграла функции y=(x^3-2x^2)/(x-2) от 3 до 4 равно 12 1/3.

Объяснение:

Вспомним правила интегрирования и формулу Ньютона-Лейбница, которые нам понадобятся:

$\displaystyle \bf \bigstar \int\limits^b_a {f(x)} \, dx = F(x) \ \Big |^b_a = F(b)-F(a) \\\\ \bigstar \int cos (kx+b) \ dx = \frac{1}{k} \cdot sin(kx+b)+C \\\\ \bigstar \int x^n \ dx = \frac{x^{n+1}}{x+1} +C, \ x\neq (-1)$

Применяем вышеуказанные правила нахождения неопределённых интегралов и формулу Ньютона-Лейбница.

$\displaystyle 1) \int\limits^\frac{\pi}{4} _\frac{\pi}{12} {\cos(2x)} \, dx = \frac{1}{2}\cdot\sin(2x) \ \Big| ^\frac{\pi}{4} _\frac{\pi}{12} = \frac{1}{2}\sin \Big( 2\cdot\frac{\pi}{4}\Big) - \bigg( \frac{1}{2}\sin \Big( 2\cdot\frac{\pi}{12}\Big) \bigg)=\\\\ = \frac{1}{2}\sin \Big(\frac{\pi}{2}\Big) - \frac{1}{2}\sin \Big(\frac{\pi}{6}\Big) =\frac{1}{2} \cdot 1-\frac{1}{2}\cdot \frac{1}{2} = \frac{1}{2} -\frac{1}{4} = \frac{1}{4} = 0.25$

Значение определённого интеграла функции y=cos(2x) от π/12 до π/4 равно 0.25.

$\displaystyle 2) \int\limits^4_3 {\frac{x^3-2x^2}{x-2} } \, dx = \int\limits^4_3 {\frac{x^2(x-2)}{x-2} } \, dx = \int\limits^4_3 {x^2} \, dx = \frac{x^{2+1}}{2+1} \ \Big|^4_3= \frac{x^3}{3} \ \Big |^4_3 =\\\\ = \frac{4^3}{3} - \frac{3^3}{3} =\frac{64}{3}-3^2 = 21\frac{1}{3} - 9 = 12\frac{1}{3}$