Алгебра, вопрос задал Levilevilevi , 7 лет назад

№65. Это одно задание

Приложения:

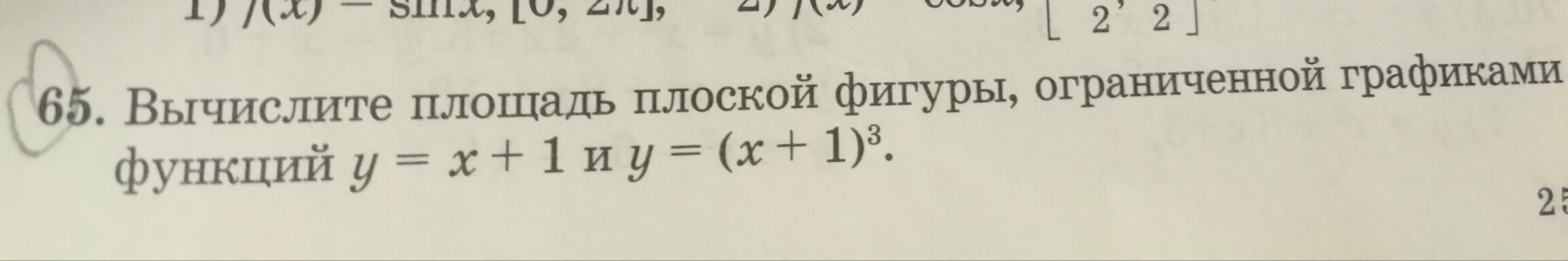
Ответы на вопрос

Ответил NNNLLL54

$65.; ; S_1=intlimits^0_{-1}(x+1-(x+1)^3), dx=Big (frac{(x+1)^2}{2}-frac{(x+1)^4}{4}Big )Big |_{-1}^0= \\=frac{1}{2}-frac{1}{4}-0=frac{1}{4}\\S_2=2cdot S_1=frac{1}{2}\\1.; ; S=intlimits^{-1}_{-3}(1-(x^2+4x+4)), dx=intlimits^{-1}_{-3}(1-(x+2)^2), dx=\\=Big (x-frac{(x+2)^3}{3}Big )Big |_{-3}^{-1}=-1-frac{1}{3}-(-3+frac{1}{3})=2-frac{2}{3}=1frac{1}{3}$

$2.; ; S=intlimits^{1}_{-1}(2-(1-x^3)), dx=intlimits^1_{-1}(1+x^3), dx=Big (x+frac{x^4}{4}Big )Big |_{-1}^1=\\=1+frac{1}{4}-(-1+frac{1}{4})=2\\3.; ; S=intlimits^{1}_{-2}(-x^2+4-(x+2)), dx=intlimits^1_{-2}(-x^2-x+2), dx=(-frac{x^3}{3}-frac{x^2}{2}+2x)Big |_{-2}^1=\\=(-frac{1}{3}-frac{1}{2}+2)-(frac{8}{3}-2-4)=frac{27}{6}\\4.; ; S=intlimits^1_0(1+2x-x^2)-(x^2+1)), dx=intlimits^1_0(-2x^2+2x), dx=\\=(-frac{2x^3}{3}+x^2)Big |_0^1=-frac{2}{3}+1= frac{1}{3}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА ДОПИШИ ВОПРОСЫ И НУЖНЫЕ ГЛАГОЛЫ ПАУЧОК(...) ... , ... . ВЕТЕР (...) ... , ... .

Другие предметы, 1 год назад

Напишіть всі книги про Бізнес та психологію Успіху.

Литература, 7 лет назад

опишите картину не меньше 7 предложений...

Алгебра, 7 лет назад

Помогите пожалуйста!!! Не могу разобраться...

Математика, 8 лет назад

вычислите объем прямоугольного параллепипеда ( в дм³), если его измерения равны : a= 4,2 дм, b=58 см, c=350мм...

Математика, 8 лет назад

SOS!! не только ответ а пример...