62 балла даю помогите прошу
Приложения:
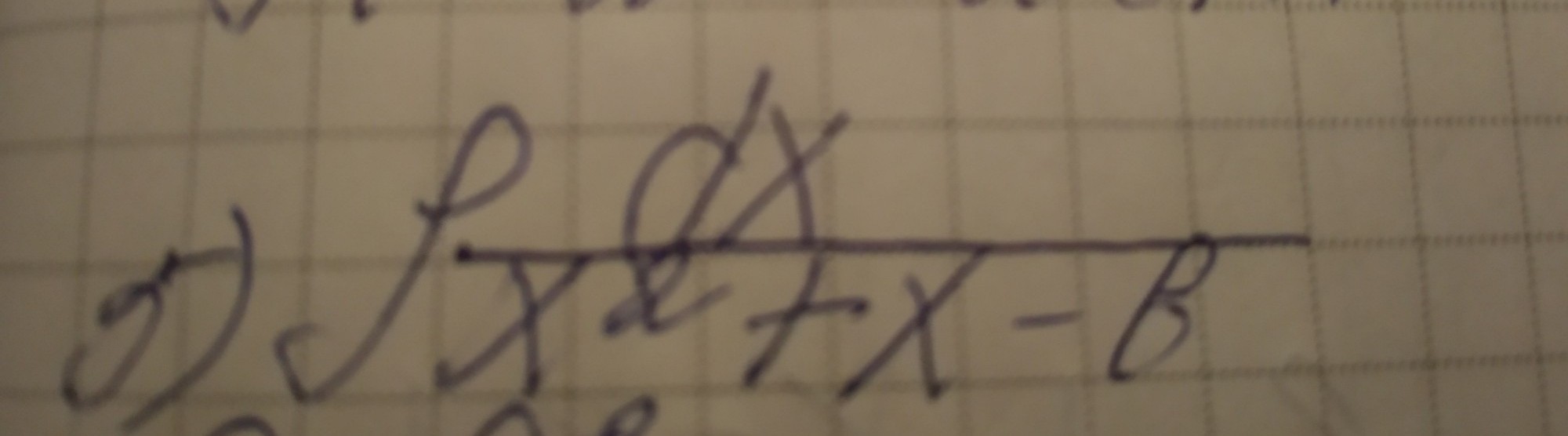
Ответы на вопрос
Ответил sangers1959
0
∫(dx/(x²+x-6))=∫dx/(x²+2*x*(1/2)+1/4-1/4-6)=∫(dx/((x+1/2)²-25/4)=
=∫(dx/(-(5/2)²-(x+1/2)²).
Используем формулу "Высокого логарифма":
∫(dx/(a²-x²)=(1/(2a))*(ln|a+x|/ln|a-x|)+C x≠a
(1/(2*5/2))*(ln|(-5/2+x+1/2)|/ln|(-5/2-x-1/2|)=
=(ln|x-2|/ln|-x-3|)/5==(ln|x-2|/ln|-(x+3)|)/5=(ln|x-2|/ln|x+3|)/5.
Ответил Аноним
0
огромное
Ответил Аноним
0
тебе
Ответил sangers1959
0
Удачи.
Ответил Аноним
0
)))
Ответил sangers1959
0
Ещё исправил. Это уже окончательный ответ.
Новые вопросы