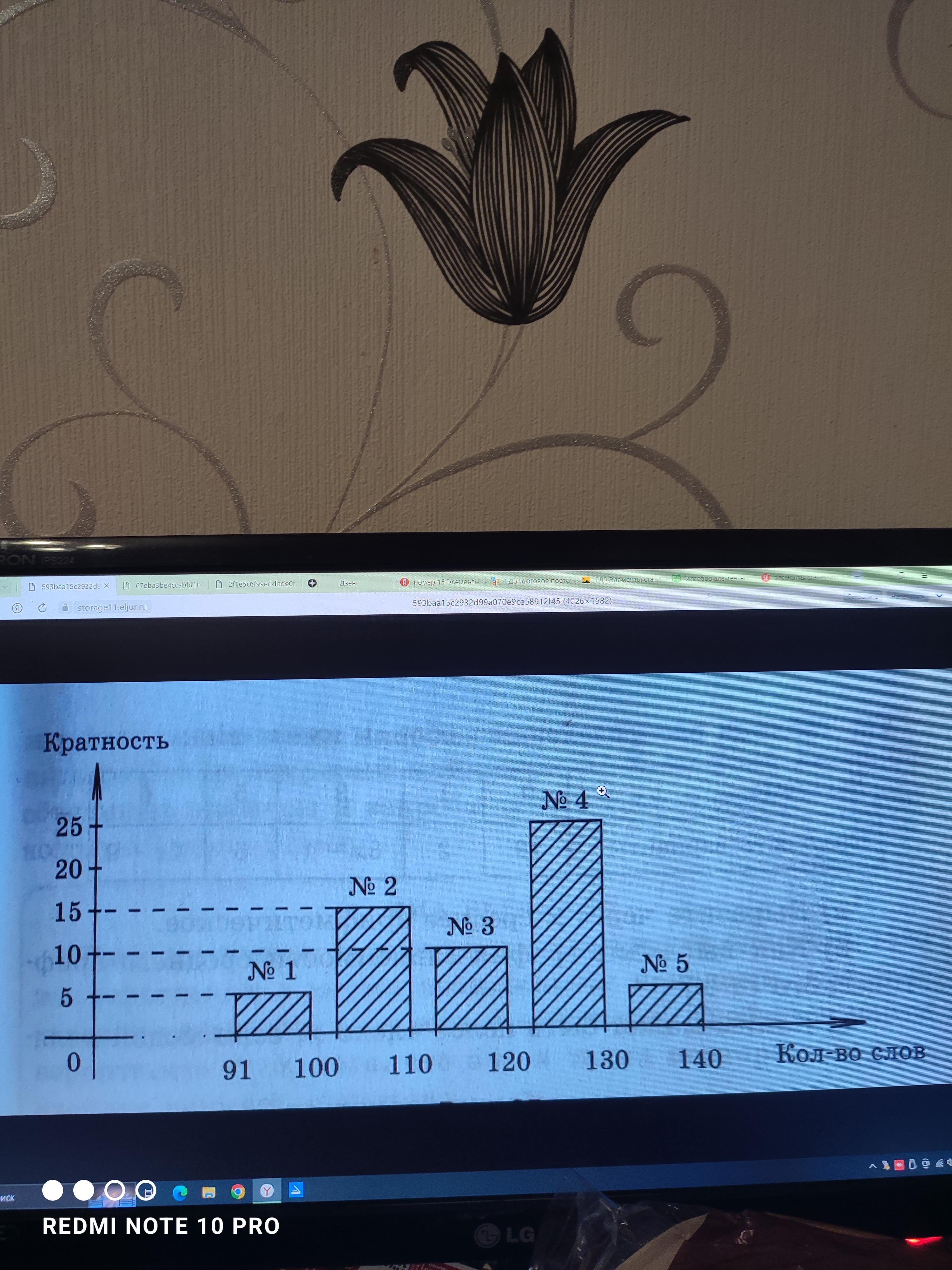
. 60 девятиклассников проверили на скорость чтения (количество слов за минуту чтения). Полученные данные сгруппировали по пяти участкам: № 1 – [91;100], № 2 - [101;110], № 3 - [111;120], № 4 - [121;130], № 5 - [131;140]. Получилась гистограмма кратностей. Приблизительно оцените: а) размах; б) моду; в) среднее арифметическое выборки; г) объясните, почему ответы лишь приблизительные. №10. (Продолжение упражнения 2.) Найдите: а) размах; б) моду; в) среднее арифметическое для экспериментальных выборок.

Ответ:

Давайте начнем с анализа данных эксперимента:

Группа № 1: 91-100

Группа № 2: 101-110

Группа № 3: 111-120

Группа № 4: 121-130

Группа № 5: 131-140

Теперь рассмотрим значения:

a) Размах - это разница между наибольшим и наименьшим значениями в выборке.

Размах ≈ 140 - 91 = 49 (слово "приблизительно" указывает на то, что мы не имеем точных значений и можем дать только приблизительную оценку).

б) Мода - это значение или диапазон значений, которые встречаются наиболее часто. Мода при этом может быть приблизительно оценена как середина диапазона для каждой группы, то есть:

- Группа № 1: Мода ≈ (91+100)/2 = 95.5

- Группа № 2: Мода ≈ (101+110)/2 = 105.5

- Группа № 3: Мода ≈ (111+120)/2 = 115.5

- Группа № 4: Мода ≈ (121+130)/2 = 125.5

- Группа № 5: Мода ≈ (131+140)/2 = 135.5

в) Среднее арифметическое - это среднее значение всех данных в выборке. Так как данные у нас представлены интервалами, то среднее арифметическое также будет приблизительным, и оно будет равно среднему значению диапазонов для каждой группы:

- Группа № 1: Среднее арифметическое ≈ (91+100)/2 = 95.5

- Группа № 2: Среднее арифметическое ≈ (101+110)/2 = 105.5

- Группа № 3: Среднее арифметическое ≈ (111+120)/2 = 115.5

- Группа № 4: Среднее арифметическое ≈ (121+130)/2 = 125.5

- Группа № 5: Среднее арифметическое ≈ (131+140)/2 = 135.5

г) Ответы являются приблизительными, потому что у нас есть только диапазоны, а не точные значения скорости чтения для каждого ученика. Поэтому все результаты мы можем оценить только приблизительно