60 баллов, геометрия!
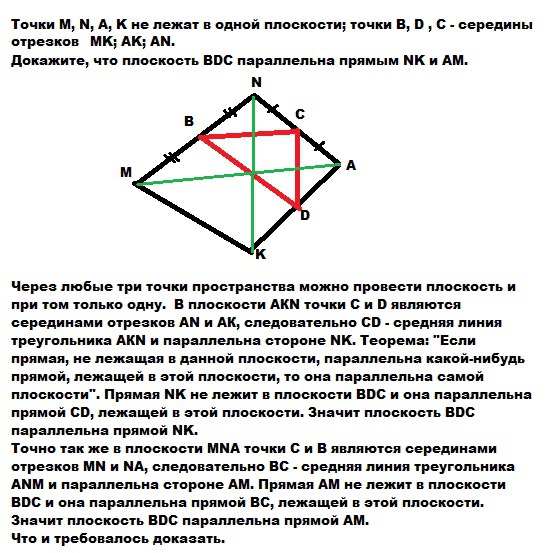
Точки M, N, A, K не лежат в одной плоскости; точки B, C , D - середины отрезков MK; AN; AK.
Докажите, что плоскость KMP параллельна прямым AC и BD.
Нужен чертеж и подробное решение!
Спасибо :3

Через любые три точки пространства можно провести плоскость и при том только одну.  В плоскости АКN точки С и D являются серединами отрезков AN и АК, следовательно СD - средняя линия треугольника АКN и параллельна стороне NK.
(Заметим, что  прямые СD и NK лежит в плоскости АКN).
Теорема: "Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости".
Заметим, что  прямая СD  лежит в плоскости BDC.
Прямая NK не лежит в плоскости ВDC и она параллельна прямой СD, лежащей в этой плоскости.
Значит плоскость ВDC параллельна прямой NK.
Точно так же в плоскости МNА точки С и В являются серединами отрезков МN и NА, следовательно ВС - средняя линия треугольника АNМ и параллельна стороне АМ. Прямая АМ не лежит в плоскости ВDC и она параллельна прямой ВС, лежащей в этой плоскости.
Значит плоскость ВDC параллельна прямой АМ.
Что и требовалось доказать.