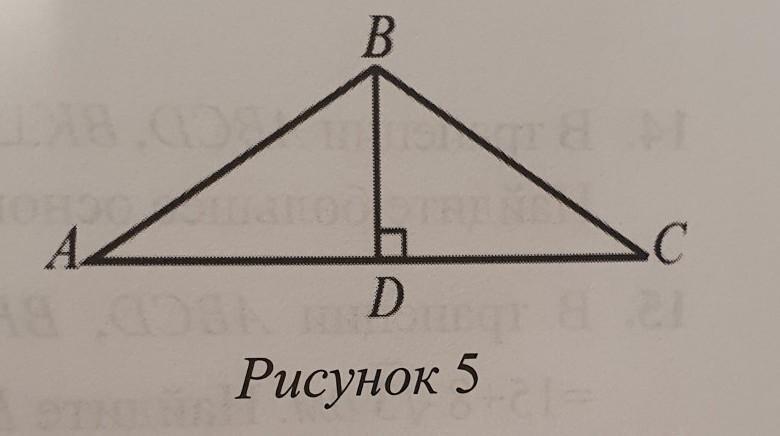
6. Периметр равнобедренного треугольника с углом при вершине 120° 16+8 √3 см. Найдите площадь треугольника ABC (рисунок 5)​

Ответ: 32√3 cm²

Объяснение:

∡В=120°  АВ=ВС ,  P(ΔABC)= 16+8 √3 см

S(ΔABC)=??

Обозначим АВ=ВС=х  .  

Рассмотрим ΔABD .  ∡ABD=120°/2=60° (В равнобедренном треугольнике высота, проведенная к основанию является также биссектрисой и медианой.

=> AD=AB*sin∡ABD =x*√3/2

=> AC=2*AD=x*√3

=> P(ΔABC)= 16+8√3 =x+x+x√3 = x(2+√3)

=> 8(2+√3)=x(2+√3) => x=8

=> S(ΔABC)= AB*BC*sin∡ABC/2= 8*8*√3/2/2= 32√3 cm²

Ответ:

решение на фото

Объяснение: