(50 балов)Два внешних угла треугольника при разных вершинах равны. Периметр треугольника равен 60 см, а одна из его сторон больше другого на 10 см. Найди оставшиеся стороны треугольника. (рассмотреть всевозможные случаи)

Ответ:

1. Стороны треугольника равны:

2. Стороны треугольника равны:

Объяснение:

Требуется найти  оставшиеся стороны треугольника. (рассмотреть всевозможные случаи)

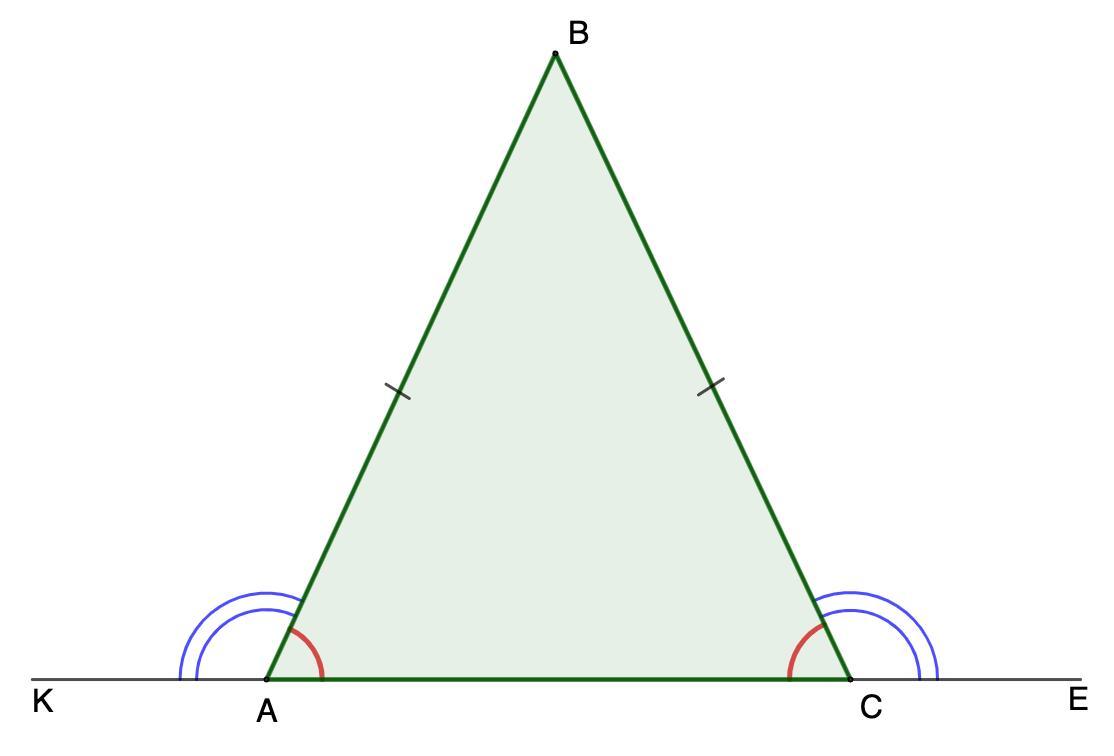
Дано: ΔАВС.

∠KAB = ∠ВСЕ - внешние;

Р (АВС) = 60 см.

Одна из сторон больше другой на 10 см.

Найти: стороны треугольника (рассмотреть всевозможные случаи).

Решение:

Рассмотрим ΔАВС.

∠KAB = ∠ВСЕ - внешние

• Смежные угла в сумме равны 180°.

⇒ ∠ВАС = 180° - ∠KAB

    ∠ВСА = 180° - ∠ВСЕ

• Если правые части равенства равны, то равны и левые.

⇒ ∠ВАС = ∠ВСА

• Если в треугольнике два угла равны, то этот треугольник равнобедренный.

⇒  ΔАВС - равнобедренный.

АВ = ВС.

1. Первый случай.

Пусть АВ = ВС = х см, тогда АС = (х + 10) см

• Периметр - сумма длин всех сторон.

Р (АВС) = АВ + ВС + АС

60 = х + х + х + 10

3х = 50

Стороны треугольника равны:

2. Рассмотрим второй случай.

Пусть АС = х см, тогда АВ = ВС = (х + 10) см

Р (АВС) = АВ + ВС + АС

60 = х + 10 + х + 10 + х

3х = 40

Стороны треугольника равны: