50 балов даю!!!!!
У рівнобічну трапецію вписано коло. Знайдіть площу трапеції, якщо бічна сторона точкою дотику ділиться на відрізки 4 см і 9 см.
Ответы на вопрос
Ответил Пеппер
2
Відповідь:
120 см²
Пояснення:
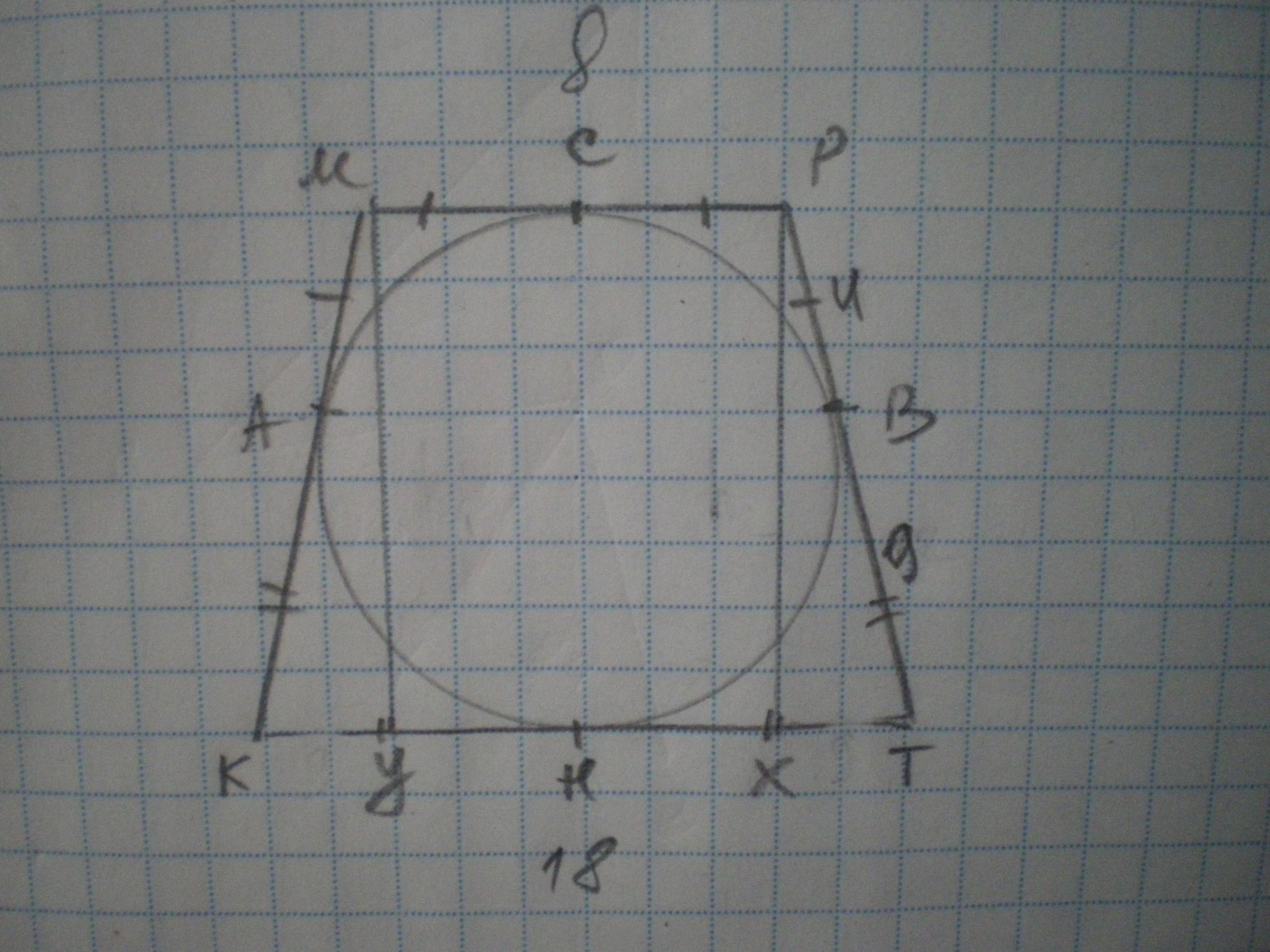
Дано: КМРТ - трапеція, АМ=РВ=4 см, АК=ВТ=9 см. Знайти S(КМРТ).
За властивістю дотичної до кола, відрізки дотичних проведені до кола з однієї точки, рівні.
Трапеція рівнобедрена за умовою, тому АМ=МС=СР=РВ=4 см;
АК=КН=НТ=ВТ=9 см.
Отже МР=4+4=8 см; КТ=9+9=18 см.
Проведемо висоти МУ та РХ, ХУ=МР=8 см, КУ=ТХ=(18-8):2=5 см.
Розглянемо ΔРТХ - прямокутний, РТ=4+9=13 см.
За теоремою Піфагора РХ=√(РТ²-ТХ²)=√(169-25)=√144=12 см.
S(СКМТ)=(8+18):2*12=15*12=120 см²
Приложения:
mashhryl:
Я ТОЛЬКО ЧТО ДОБАВИЛА НОВОЕ ЗАДАНИЕ СДЕЛАЙТЕ ПОЖАЛУЙСТА
S(СКМТ)=(8+18):2*12=15*12=120 см² тут так: (8+18):2*12=13*12=156 см² ))))
Новые вопросы
Алгебра,
1 год назад
Математика,
1 год назад
Русский язык,
1 год назад
Русский язык,
1 год назад
Биология,
6 лет назад