50 баллов нужно решение срочно 50 баллов!!!
пожалуйста с полной росписью
Приложения:
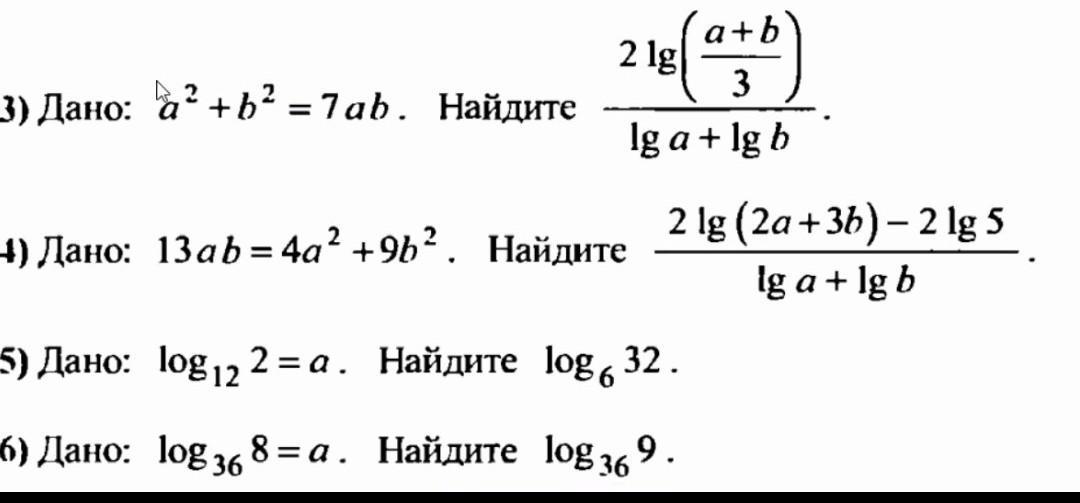
Ответы на вопрос
Ответил Universalka
0
Аноним:
Universalka, здравствуйте! у меня в профиле 4 вопроса по алгебре, можете помочь пожалуйста?
Новые вопросы
Литература,
11 месяцев назад
Литература,
11 месяцев назад
Алгебра,
1 год назад
Химия,
1 год назад
Русский язык,
6 лет назад
Математика,
6 лет назад