50 БАЛЛОВ Найдите экстремумы функции и исследуйте на монотонность. Нужно нарисовать + и - на интервалах. Выделенное:
Приложения:
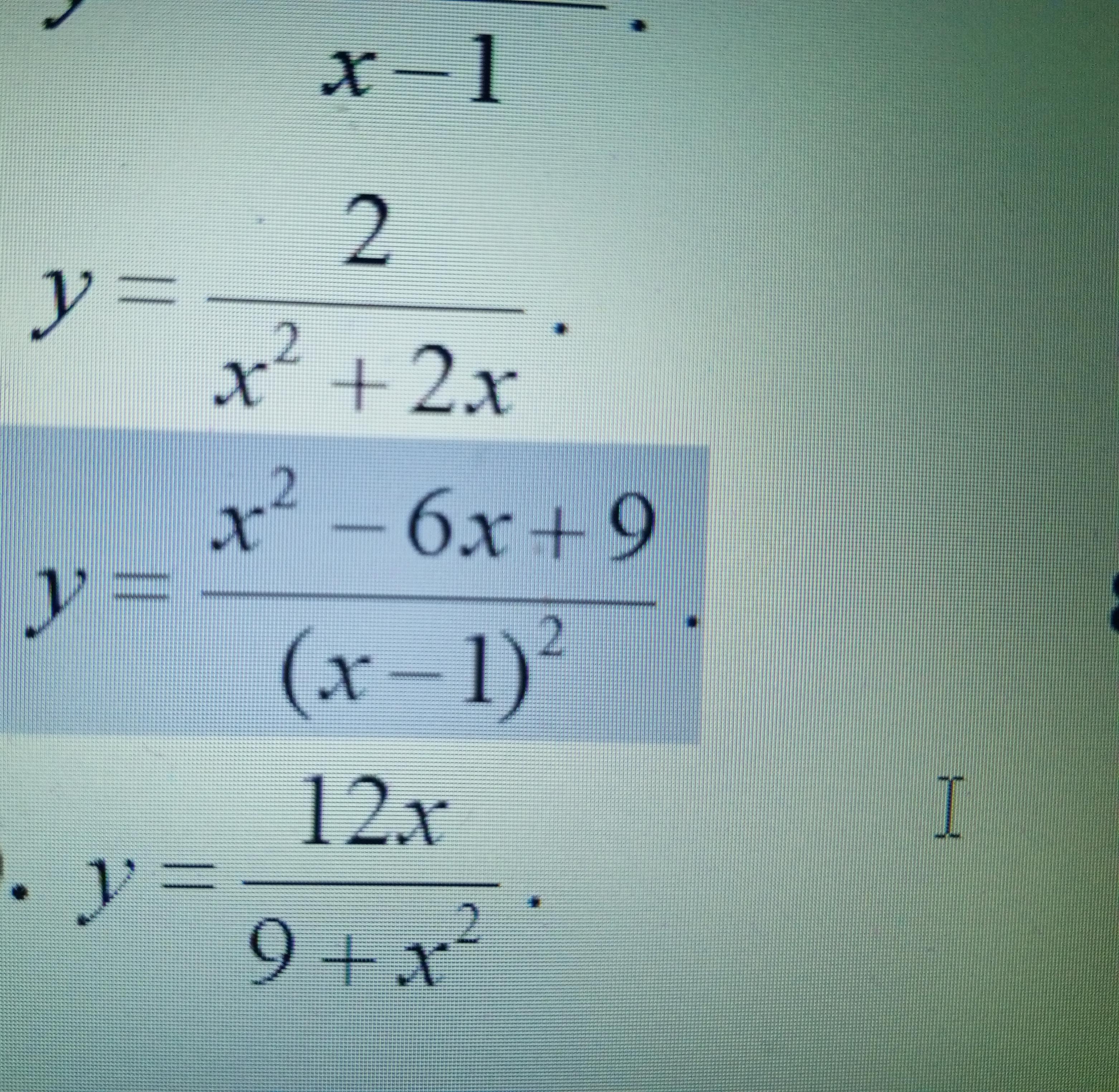
Ответы на вопрос
Ответил plaJohan
1
Ответ:
Пошаговое объяснение:
1. Монотонность.
D(y) = { x ∈ R : x ≠ 1 }, т.к. (x-1)²≠0.
E(y) = { y ∈ R : y ≥ 0 }, т.к. (-x)²>0; -x/-x > 0.
2. Экстремумы.
Первая производная.
Нуль-функция производной.
y' = 0
4(x-3)=0, т.к. только верхняя часть должна быть равна нулю.
x=3
Экстремум.
Xэ= 3
Yэ= 0, т.к. 9-18+9=0 (верхняя часть уравнения функции).
Т.К. E(y) = { y ∈ R : y ≥ 0 }, Хэ(3;0) - MIN.
3. Интервалы монотонности
(-∞;1) (1;3) (3;+∞)
y' + - +
y ↑ ↓ ↑
Новые вопросы
Українська мова,
11 месяцев назад
Математика,
11 месяцев назад
Французский язык,
11 месяцев назад
Алгебра,
11 месяцев назад
Английский язык,
6 лет назад