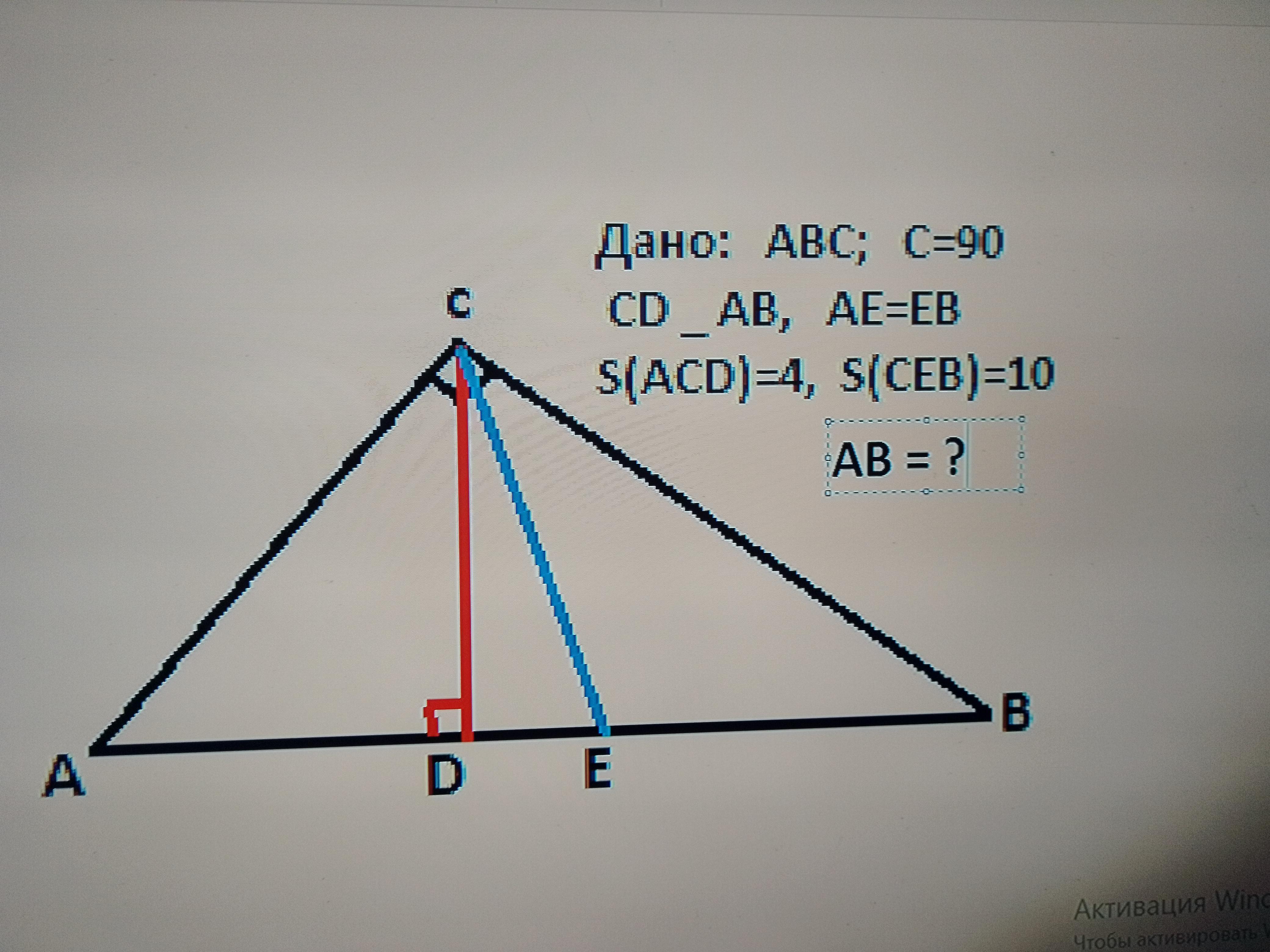
5. В прямокутному трикутнику AВС ( С = 90°) проведено висоту CD і медіану СЕ. Площі трикутників АСD і ЕСВ дорівнюють відповідно 4 см² і 10 см². Знайти AB.​

Ответ:

Объяснение:

Зная свойство медианы ∆ ( она делит его на два равно великих) имеем что $(СЕВ)=$(АЕС)=10

$(АЕС)=0,5*АЕ*СД=10. ,АЕ=АВ/2 подставим и выразим

СД= 10/ (0,5 АВ/2)= 40/ АВ. . [1].

Из ∆ АСД. $(АСД)=0,5АД*СД= 4

СД= 4/(0,5АД) = 8/АД. [2]

40/АВ = 8/АД

АД= АВ/5.

Из ∆CDE

S(CДE)=0,5*ДE*CD=6,.

CD=6/0,5ДE= 12/ДЕ. [3]

ДЕ=АВ/2 - АД. из предыдущего АД=АВ/5. => ДЕ=0,3АВ. [4]

,Используя св-во высоты прямоугольного треугольника,

СД^2 = АД*ЕД. [5]

Подставляем [3] и [4] получаем

(40/АВ)^2 =(АВ/5)*(0,3АВ)

1600/АВ^2 = АВ^2/0,06

АВ^4 = 1600*0,06=96=16*6

АВ= {4√96}=2*{4√6}

Два корня 4 степени их 6