5. У рівнобічній трапеції менша основа дорівнює 1 см, бічна сторона √3
см, а більший кут становить 150°. Знайдіть діагональ трапеції.

Ответ: =√7 cm

Объяснение:

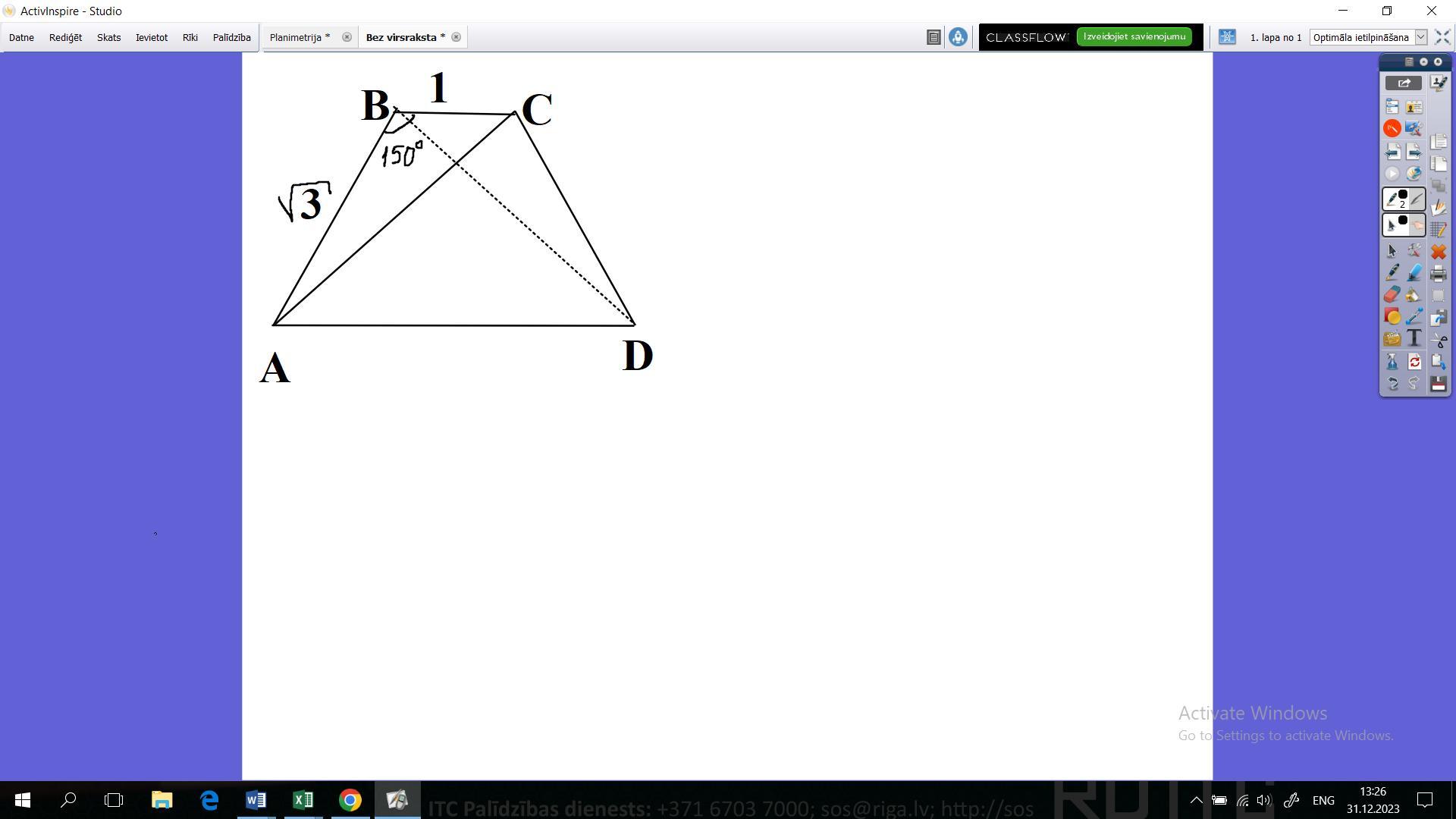
Меньшая основа ВС, боковая сторона АВ и диагональ АС образуют треугольник с тупым углом В= 150° напротив диагонали АС.

По теореме коcинусов   (cos 150°= -√3/2

АС²=ВС²+АВ²-2·АВ·ВС·cos∡B = 1+3-2√3·(-√3/2) =4+3=7

=> AC=√7 cm

Так как трапеция  равнобочная,то ее диагонали равны

Ответ:

√7 см.

Объяснение:

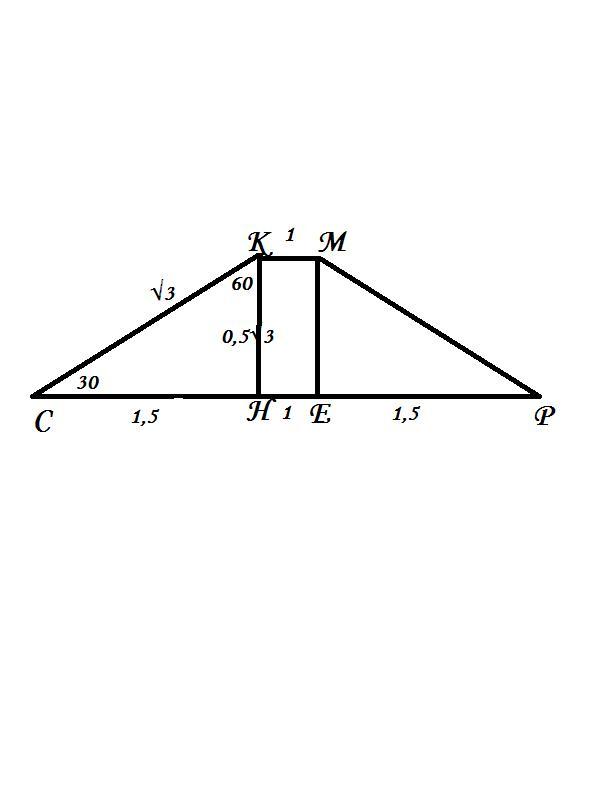
Дано: СКМР - трапеція, СК=МР=√3 см, КМ=1 см, ∠СКМ=150°. КР - ?

Проведемо висоти КН і МЕ. ΔСКН - прямокутний, ∠СКН=150-90=60°;

∠С=90-60=30°;   КН=1/2 СК за властивістю катета, що лежить проти кута 30°;  КН=ЕМ=1/2 СК=0,5√3 см.

СН²=ЕР=(√3)²-(0,5√3)²=3-0,75=2,25;  СН=ЕР=√2,25=1,5 см.

РН=ЕН+РЕ=1+1,5=2,5 см.

КР²=КН²+РН²=(0,5√3)²+2,5²=0,75+6,25=7; КР=√7 см