Математика, вопрос задал margarita16031986 , 11 месяцев назад

5. Сумма первых трех членов геометрической прогрессии равна 26, знаменатель прогрессии равен 3. Найдите сумму первых шести членов этой прогрессии.

Ответы на вопрос

Ответил Alnadya

Решение .

Сумма первых трёх членов геометрической прогрессии со

знаменателем q = 3 равна 26 ⇒

$\bf b_1+b_1q+b_1q^2=b_1+3b_1+9b_1=26\ \ \ \Rightarrow \ \ \ 13b_1=26\ \ ,\ \ b_1=2\\\\\\S_6=\dfrac{b_1\, (q^6-1)}{q-1}=\dfrac{2\, (3^6-1)}{3-1}=\dfrac{2\cdot 728}{2}=728$

Приложения:

Предыдущий вопрос

Следующий вопрос

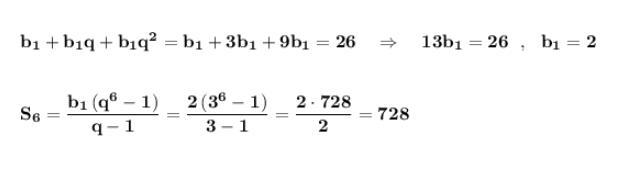
Новые вопросы

Литература, 7 месяцев назад

14. Установіть відповідність між казками та їх героями (2 бали кожне завдання) 1. Якоб і Вільгельм Грімм. « Пані Метелиця» А. Панночка, Мар’яна, Петрусь. 2. Шарль Перро. «Попелюшка, або Кришталевий...

Английский язык, 7 месяцев назад

Помогите пожалуйста даю 20 баллов срочно...

Литература, 11 месяцев назад

6. Что стало с царевной из «Сказки о мёртвой царевне…», после того как поела яблоко: А) бросив терем наутёк, молвила, что дар не впрок Б) за горло ухватилась, пала, еле шевелилась В) головой на лавку...

Английский язык, 11 месяцев назад

ВСЕ ПРАВИЛЬНО 19/22 ОШИБКИ НА ГОВОРЕНИЕ Listening Task. Listen to the conversation between Harry and Elizabeth twice. Transcript for listening task can be found ofter the mark scheme. Teacher reads...

Алгебра, 6 лет назад

Четверо школьников из разных городов уезжая из лагеря решили обменяться открытками с адресами .Сколько открыток было роздано...

Математика, 6 лет назад

3х-3=2х+4 срочнооооо...