Алгебра, вопрос задал veronikavitaly , 6 лет назад

5. Найдите частное решение уравнения у"+7у'+12у=0 удовлетворяющее начальным условиям у(0)-1, у (0)--2.

Приложения:

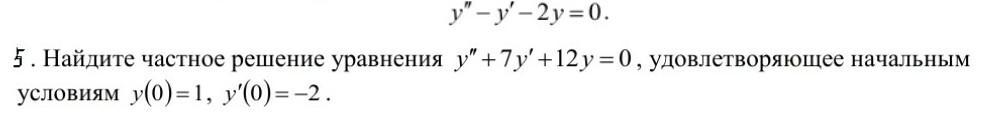
Ответы на вопрос

Ответил hote

Дано

$\displaystyle y``+7y`+12y=0$

составим характеристическое уравнение

$\displaystyle k^2+7k+12=0\\\\D=49-48=1\\\\k_{1.2}=\frac{-7 \pm 1}{2}\\\\k_1=-4; k_2=-3$

тогда общее решение

$\displaystyle y=C_1*e^{-4x}+C_2*e^{-3x}$

теперь частное решение при условии

$\displaystyle y(0)=1; y`(0)=-2$

$\displaystyle y(0)=C_1*e^{-4*0}+C_2*e^{-3*0}=C_1+C_2=1$

$\displaystyle y`(0)=-4C_1*e^{-4*0}-3C_2*e^{-3*0}=-4C_1-3C_2=-2\\\\\left \{ {{C_1+C_2=1} \atop {-4C_1-3C_2=-2}} \right.$

$\displaystyle C_1=1-C_2\\\\-4(1-C_2)-3C_2=-2\\\\-4+4C_2-3C_2=-2\\\\C_2=2; C_1=1-2=-1$

частное решение

$\displaystyle y=-e^{-4x}+2*e^{-3x}$

Новые вопросы

Русский язык, 1 год назад

Английский язык, 1 год назад

Алгебра, 6 лет назад

Английский язык, 6 лет назад

География, 8 лет назад

Математика, 8 лет назад