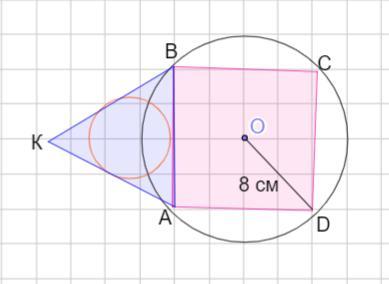
5. Квадрат вписан в окружность радиуса 8 см. На стороне квадрата построен правильный треугольник. Найдите: а) радиус окружности, вписанной в этот треугольник. b) площадь этого треугольника.
Ответы на вопрос
Ответ:
а) см ; б) 32 √3 см².
Объяснение:
Квадрат вписан в окружность радиуса 8 см. На стороне квадрата построен правильный треугольник . Найти: а) радиус окружности вписанной в этот треугольник. б) площадь этого треугольника.
Дан квадрат ABCD вписанный в окружность, тогда окружность описана около квадрата.
Радиус окружности, описанной около квадрата, определяется по формуле:
где а -сторона квадрата. Тогда найдем сторону квадрата
см
На стороне АВ квадрат построен Δ АВК - правильный.
Значит, стороны этого треугольника все равны по 8√2 см.
Радиус окружности, вписанной в правильный треугольник, определяется по формуле:
где а - сторона треугольника.
Тогда
см
Найдем площадь треугольника как полупроизведение периметра треугольника на радиус вписанной окружности.
Периметр- это сумма длин всех сторон
P = 3· 8√2= 24√2 cм.
Площадь треугольника равна 32 √3 см².
#SPJ1