5. Чому дорівнює радіус кола, вписаного в правильний шестикут- ник, менша діагональ якого дорівнює 12 см? А) 6 см; Б) 6 3 см; B) 2 3 см; Г) 12 см. с​

Ответ:

А) 6 см

Объяснение:

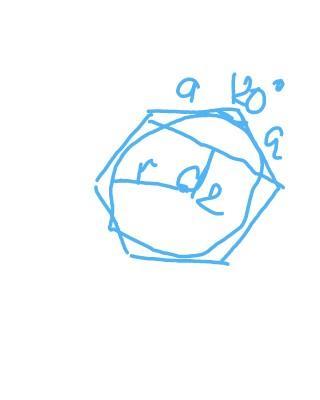
r - радиус описанной окружности

а - сторона

d2 =12 cм- меньшая диагональ

r=(a×корень3) /2

Всё углы правильного 6 ти угольника равны 120 гродусов

Рассмотрим тр-к с боковыми сторонами а и основанием d2.Он - равнобедренный.

Угол между боковыми сторонами равен 120 гродусов, тогда углы при основании равны (180-120)/2=30 градусов.

По теореме синусов :

(d2) /sin120=a/sin30

12/ (корень3/2)=а/(1/2)

12×2 / корень3=а×2

24/корень3=а×2

а=24/корень3 :2=24/корень3×1/2=

=12/корень3=

=(12×корень3) /(корень3 ×корень3) =

=12/3×корень3 =4×корень3 см

r=(4корень3×корень3) /2=4×3 /2=6 см