Алгебра, вопрос задал nlikachev , 7 лет назад

40 баллов, Тригонометрия ,помогите пожалуйста, если не знаете, то не пишите

Приложения:

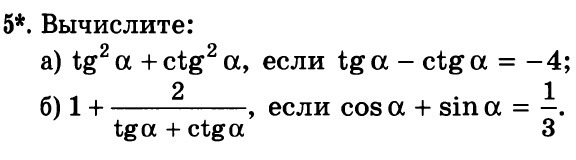
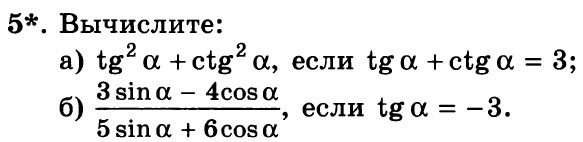
Ответы на вопрос

Ответил Universalka

$(tg alpha -Ctg alpha ) ^{2}=(-4) ^{2}\\tg ^{2} alpha -2tg alpha Ctg alpha +Ctg ^{2} alpha =16\\tg ^{2} alpha +Ctg ^{2} alpha =16+2tg alpha Ctg alpha =16+2*1=18$

$(Cos alpha +Sin alpha ) ^{2} =( frac{1}{3}) ^{2}\\Cos ^{2} alpha +2Sin alpha Cos alpha +Sin ^{2} alpha = frac{1}{9}\\2Sin alpha Cos alpha = frac{1}{9} -(Sin ^{2} alpha +Cos ^{2} alpha )\\2Sin alpha Cos alpha = frac{1}{9}-1=- frac{8}{9} \\\1+ frac{2}{tg alpha +Ctg alpha }=1+ frac{2}{ frac{Sin alpha }{Cos alpha }+ frac{Cos alpha }{Sin alpha } }=1+ frac{2}{ frac{Sin ^{2} alpha +Cos ^{2} alpha }{Sin alpha Cos} }=1+ 2Sin alpha Cos alpha =1- frac{8}{9} = frac{1}{9}$

$(tg alpha +Ctg alpha ) ^{2} =3 ^{2}\\tg ^{2} alpha +2tg alpha Ctg alpha +Ctg ^{2} alpha =9\\tg ^{2} alpha +Ctg ^{2} alpha =9-2tg alpha Ctg alpha =9-2=7$

$frac{ frac{3Sin alpha }{Cos alpha } - frac{4Cos alpha }{Cos alpha } }{ frac{5Sin alpha }{Cos alpha } + frac{6Cos alpha }{Cos alpha } } = frac{3tg alpha -4}{5tg alpha +6} = frac{3*(-3)-4}{5*(-3)+6}= frac{-13}{-9}=1 frac{4}{9}$

Ответил nlikachev

Ой, а по проще можно? хд)

Ответил Universalka

Попроще это как, 2+3=5?

Ответил nlikachev

Нет, просто, откуда синус в квадрате + косинус в квадрате ,2-ое выражение?

Ответил Аноним

5*
a) Преобразуем выражение tgα - ctgα = -4
Возведём его в квадрат
tg²α - 2tgα·ctgα + ctg²α = 16
tg²α - 2 · 1 + ctg²α = 16
tg²α + ctg²α = 18
б)то же самое: возведём в квадрат cosα + sinα = 1/3
cos²α + 2sinα·cosα + sin²α = 1/9
1 + sin2α = 1/9
sin 2α = -8/9
а теперь преобразуем другое выражение
1 + 2/(tgα + ctgα) = 1 + 2(sinα/cosα + cosα/sinα) =
= 1 + 2sinα ·cosα/(sin²α + cos²α) =
= 1 + sin2α = 1 - 8/9 = 1/9
5*
a) tg²α + ctg²α = tg²α + ctg²α + 2tgα · ctgα - 2 =
= (tgα + ctgα)² - 2 = 3² - 2 = 7
б) (3sinα - 4cosα)/(5sinα + 6cosα) =
= (3tgα-4)/ 5tgα + 6) = (3 ·(-3) - 4)/(5·(-3) + 6) = 1целая 4/9

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Психология, 1 год назад

Что веришит судьбу человечества в этом мире? Некое незримое существо, или закон? Нечто подобное длани господней парящий над миром ?

Русский язык, 1 год назад

Срочно!!!! ПОМОГИТЕ ПОЖАЛУЙСТА...

Математика, 7 лет назад

Подскажите пожалуйста с ответом и как можно будет правильно и доходчиво объяснить...