40 баллов!!!
На координатной плоскости с единичным отрезком один см изобразите круг с центром в точке T (2,0) и радиусом 2 см и треугольник с вершинами K (0;0), L(0;2), M (4;0). Сколько процентов составляет площадь треугольника от площади круга? ( Ответ дайте с точностью до 1 %)
40 баллов!!!
Ответы на вопрос
Ответ:
Пошаговое объяснение:
катеты треугольника
a=4 b =2
Sтреугольника=ab/2=4*2/4=4
Sкруга=пr²=4п
(Sтреугольника/Sкруга)*100%=(4/(4п)*100%=(100/п)%≈(100/3,14)%≈32%
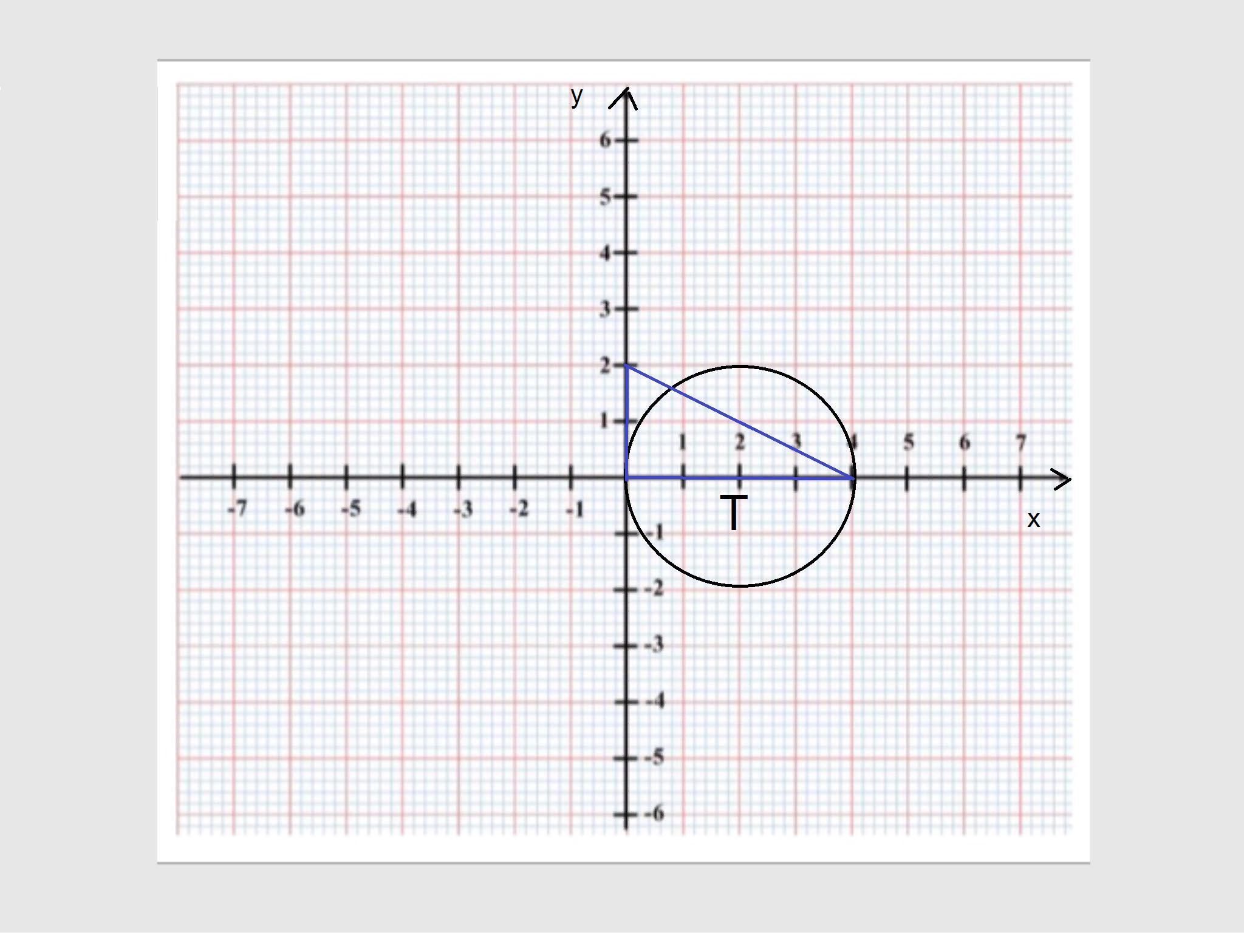
Не имею возможности рисовать, попробую аналитически рассказать, КАК нарисовать, а решить не сложно.
Итак, рисунок, поставьте ножку циркуля по оси ОХ на 4 клетки вправо. Это будет от нуля два единичных отрезка, и раствором, равным 2см, т.е. 4клетки, опишите радиусом окружность. Теперь о треугольнике. Найдите три точки - вершины треугольника, это начало координат, ноль, ноль, точка (4;0) лежит на 4ед. отрезка вправо по оси ох от начала координат, или на 8 клеток вправо, а точка эль по оси оу находится на 2ед. отрезка от начала вверх.
Соедините три вершины. Получите треугольник. Видно, что у него есть два катета 4 ед. отрезка и 2 ед. отрезка, один лежит на оси ох, другой на оси оу, площадь треугольника найдем, умножив катеты и поделя произведение надвое. т.е. 4*2/2=4/ед. кв./
Площадь круга равна ПИ эр в квадрате, т.е. π*2²=4π≈4*3,14=12,56/ед.кв./
Найдем отношение площади треугольника к площади круга и выразим ее в процентах, округлив до одного процента.
4/12,56*100%≈31,8%≈32%
