Алгебра, вопрос задал razumets09 , 1 год назад

40 баллов даб пж подробное решение

Приложения:

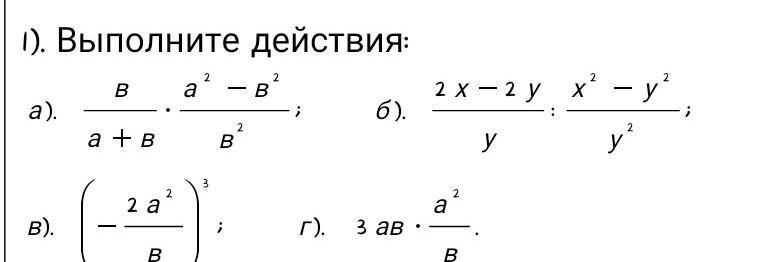
Ответы на вопрос

Ответил Alnadya

Решение.

При выполнении действий применяем свойства степеней и формулу разности квадратов .

$\displaystyle \bf a)\ \frac{b}{a+b}\cdot \frac{a^2-b^2}{b^2}=\frac{1}{a+b}\cdot \frac{(a-b)(a+b)}{b}=\frac{a-b}{b}\\\\\\b)\ \ \frac{2x-2y}{y}\, :\, \frac{x^2-y^2}{y^2}=\frac{2\cdot (x-y)}{y}\cdot \frac{y^2}{(x-y)(x+y)}=\frac{2y}{x+y}\\\\\\c)\ \ \Big(-\frac{2a^2}{b}\Big)^3=-\frac{8a^6}{b^3}\\\\\\d)\ \ 3ab\cdot \frac{a^2}{b}=\frac{3ab\cdot a^2}{b}=3a\cdot a^2=3a^3$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

История, 1 год назад

Які стосунки зі слов'янами з аварами...

Литература, 1 год назад

Помогите написать сочинение описание картины "Рожь" автора И. И. Шишкин...

Оʻzbek tili, 1 год назад

123 стр 1 машк пожалуйста...

Математика, 1 год назад

Дуже треба вирішити через 5 хвилин має бути готовим...

Геометрия, 6 лет назад

3. Равные отрезки АВ и СД пересекаются в точке О. Точка O является серединой отрезков АВ и СД. Проведены отрезки ВС и AД. Чему равен угол ВСО, если угол ДАО= 40° ...

Русский язык, 6 лет назад

помогите срочно, прям срочно!!: напишите, пожалуйста, сочинение (от 100 слов до 150) про ваше интересное путешествие ...

40 баллов даб пж подробное решение​

Ответы на вопрос

40 баллов даб пж подробное решение