4. Укажи кiлькiсть розв'язків системи нерівностей A 2; Б 3; в о; Г 4. x² +y² =16, y = x² -4. ​

Ответ:

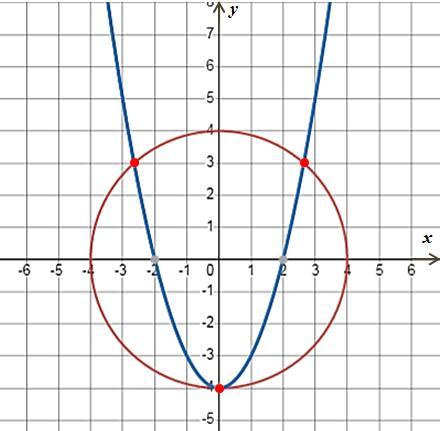
Система уравнений имеет ровно 3 решения

Объяснение:

Требуется указать количество решений системы уравнений:

.

Информация. 1) Уравнение окружности с центром в точке (x₀; y₀) и радиуса R:

(x - x₀)² + ( y - y₀)² = R².

2) Формула y = (x - x₀)² + y₀ - уравнение параболы с вершиной в точке  (x₀; y₀).

Решение. Первое уравнение системы - это уравнение окружности с центром в точке (0; 0) и радиуса 4. Второе уравнение системы - это уравнение параболы с вершиной в точке (0; -4).

По чертежу видно (см. рисунок), что окружность и парабола пересекаются в трёх точках, то есть система уравнений имеет ровно 3 решения.

#SPJ1