4. Катет прямоугольного треугольника равен 40 см, а его проекция на гипотенузу 32 см, Выполнив рисунок, найдите гипотенузу и второй катет треугольника СРОЧНО ПОМОГИТЕ ДАЮ 30 БАЛЛОВ!!!
Ответы на вопрос
Ответил natalyabryukhova
1
Ответ:
Гипотенуза равна 50 см, второй катет равен 30 см.
Объяснение:
4. Катет прямоугольного треугольника равен 40 см, а его проекция на гипотенузу 32 см, Выполнив рисунок, найдите гипотенузу и второй катет треугольника.
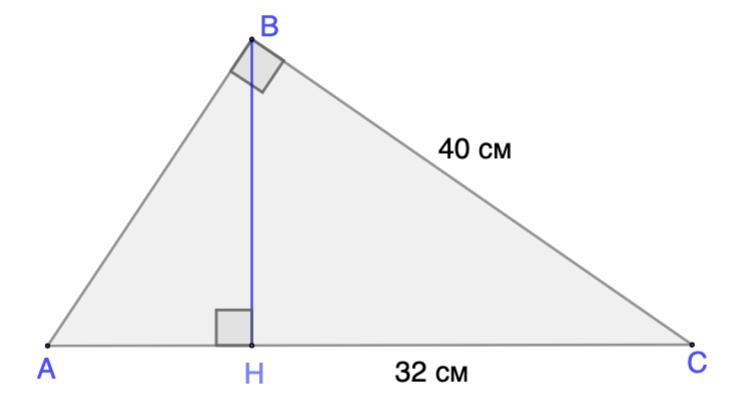
Дано: ΔАВС - прямоугольный;
ВН - высота;
ВС = 40 см; НС = 32 см
Найти: АС; АВ
Решение:
Рассмотрим ΔНВС - прямоугольный;
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
⇒ ВС² = ВН² + НС²
1600 = ВН² + 1024 ⇒ ВН² = 576 ⇒ ВН = 24 см
- Квадрат высоты, опущенной из вершины прямого угла прямоугольного треугольника на гипотенузу равен произведению проекций катетов на гипотенузу.
⇒ ВН² = АН · НС
576 = АН · 32 ⇒ АН = 576 : 32 = 18 (см)
АС = АН + НС = 18 + 32 = 50 (см)
Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора:
АС² = АВ² + ВС² ⇒ 2500 = АВ² + 1600 ⇒ АВ = 30 (см)
Гипотенуза равна 50 см, второй катет равен 30 см.
#SPJ1
Приложения:
Новые вопросы
Математика,
6 месяцев назад
Алгебра,
6 месяцев назад
Физика,
10 месяцев назад
Математика,
10 месяцев назад
Окружающий мир,
6 лет назад