Алгебра, вопрос задал Vladus0009 , 6 лет назад

4) A = x + 8
помогите

Приложения:

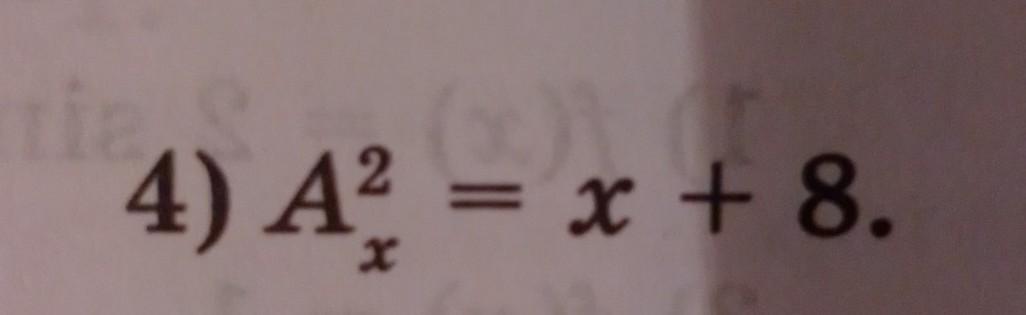
Ответы на вопрос

Ответил NNNLLL54

2

Ответ:

$A_{x}^2=x+8\ \ ,\ \ \ \ \boxed{\ A_{n}^{k}=n(n-1)\cdot ...\cdot (n-k+1)\ }\\\\x\cdot (x-1)=x+8\\\\x^2-2x-8=0\\\\x_1=-2\notin N\ ,\ x_2=4\ \ (teorema\ Vieta)\\\\Otvet:\ x=4\ .$

Ответил bb573878

0

Ответ:

Объяснение:

$\displaystyle\mathbf\\A_x^2=x+8,~~~~x\in\mathbb{N}\\\\A_n^k=\frac{n!}{(n-k)!} \\\\\\A_x^2=\frac{x!}{(x-2)!} =\frac{(x-2)!(x-1)x}{(x-2)!}=x^2-x=x+8;\\\\x^2-2x-8=0\\\\po~Vieta\\\\x_1=-2~~ne\in\mathbb{N}\\\\x_2=4\\\\Otvet:x=4$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

переведите два текста: 1) my favourites films are comedies. I like to see things thft make me laugh. 2) I like adventure stories. My favourites films have people doing lots of exciting and...

Немецкий язык, 1 год назад

сочинение на немецком языке на тему "Мой дом"...

Физика, 6 лет назад

определите путь который пролетел вертолёт за 50 минут со скоростью 60 км/ч...

Геометрия, 6 лет назад

СРОЧНО!! Стороны трапеции соотносятся как 5:1:3:8, а периметр её равен 85 см. Вычисли стороны трапеции. (Длины сторон записывай в таком же порядке, как даны в соотношении.) Ответ: первая сторона...

Математика, 8 лет назад

СРОЧНО! ПОМОГИТЕ! $frac{ 7^{-3}* 7^{9} }{ 7^{4} }$ ...

География, 8 лет назад

помогите СРОЧНО ПОЖАЛУЙСТА ЕЕ БУДЬТЕ РАВНОДУШНЫ...