Алгебра, вопрос задал DragonQueenxMILF , 6 лет назад

№3Докажите тождество

Приложения:

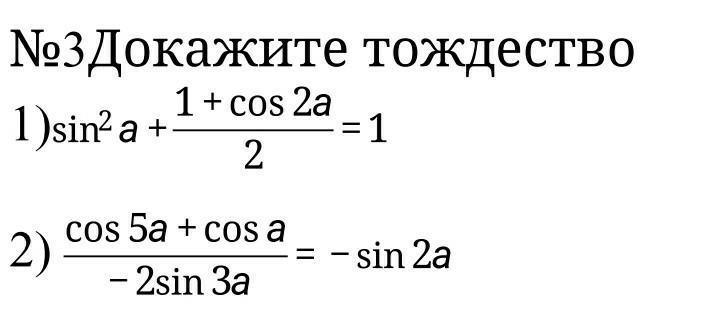
Ответы на вопрос

Ответил kamilmatematik100504

1)

Формула двойного угла

$\boxed{\cos 2a = \cos^2a-\sin ^2 a}$

Тогда

$\sin ^2 a+\dfrac{1+\cos 2a }{2} =1 \\\\\\ \sin ^2 a+ \dfrac{1+\cos^2 a -\sin ^2 a}{2} =1 \\\\\\ \sin ^2 a+\dfrac{2\cos^2a}{2} =1 \\\\\\ \sin^2a+\cos^2a =1 ~~ \checkmark$

Тождество доказано .

2)

Формула суммы

$\boxed{\cos x+\cos y = 2\cos \frac{x+y}{2} \cos \frac{x-y}{2} }$

Тогда

$\displaystyle \frac{\cos 5 a+\cos a}{-2\sin 3a } =-\sin 2a \\\\\\ \cos 5a +\cos a = 2\cdot \sin 2a \cdot\sin 3a \\\\\\ 2 \cos \frac{5a+a}{2} \cdot \cos\frac{5a-a}{2} = 2\cdot \sin 2 a\cdot \sin 3a \\\\\\\ \cos 3a \cdot \cos 2 a \neq \sin 3a \cdot \sin 2a$

Данное выражение не явлется тождеством .

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

1)Друзья попрощались и махали друг другу. 2)Алексей прикручивал коньки к валенкам и вышел на лед. 3) ребята повернули головы и всё смотрели на меня. Нужно вставить слова в предложения:...

Русский язык, 1 год назад

Спишите вставляя пропущенные буквы и обьясняя написание о или е после шипящих и ц. Сделайте вывод. Глянц_вый, свинц_вый, истощ_нноость, внуш_нный, корч_вка, свеж_ , ещ_ , жгуч_ ,туш_нка, расч_ска,...

Математика, 6 лет назад

Упражнения 1163. На координатной плоскости изобразите вектор AB, если известны координаты точек: A(0; 2), B(-3; 2). Постройте вени А, В относительно начала координат. тор CD, если точки C, D...

Право, 6 лет назад

17-річна Іванна Звернулися до Київського метрополітену із проханням прийняти її на роботу прибиральницею їй було відмовлено причиною відмови була названа норми трудового законодавства яка забороняє...

Биология, 8 лет назад

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА)))) Пастбищная цепь луга состоит из следующих звеньев (перечислены в случайном порядке!): ландыш, жук-листоед, уж, лягушка. На лугу обитает 6 особей ужа. Определите,...

Математика, 8 лет назад

помогите пожалуйста решить уравнение очень прошу...