35 баллов!!!
СРОЧНО, ПОЖАЛУЙСТА!!!
в первом номере(а и б) нужно найти производную функции
а во втором номере :найдите наибольшее и наименьшее значения функции на данном промежутке
Приложения:
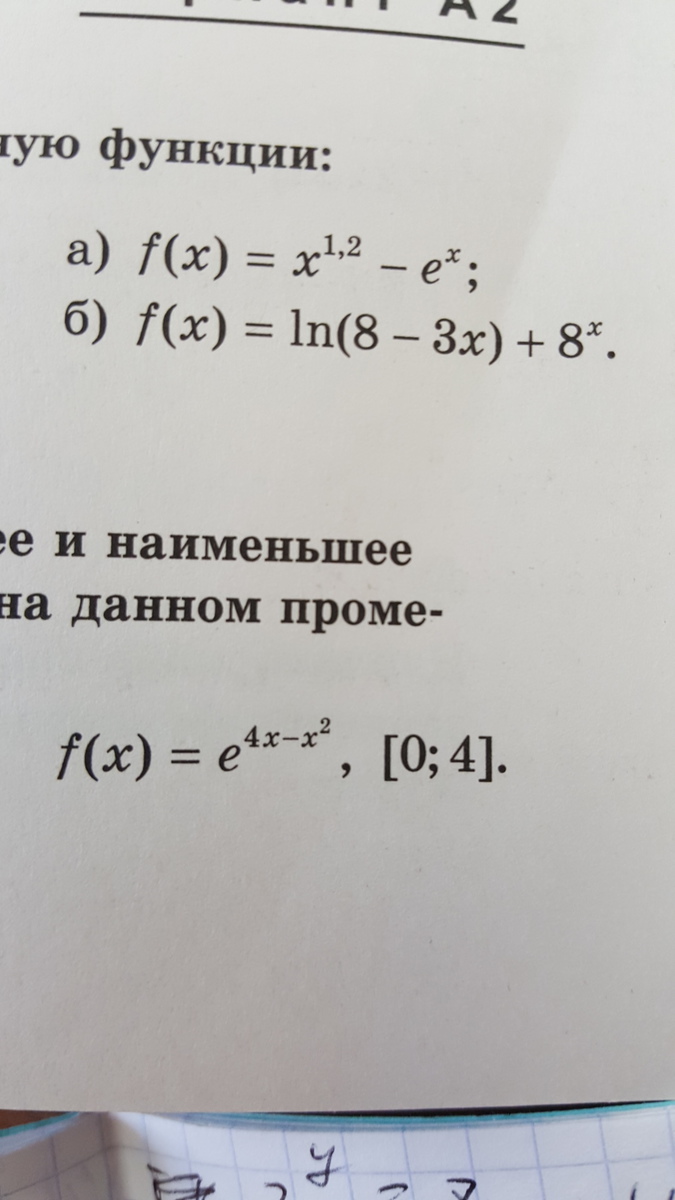
Ответы на вопрос
Ответил nKrynka
0
Решение
1.
а) f(x) = x^(1,2) - e^x
f`(x) =1,2 * x^(1,2 - 1) - e^x = 1,2 * x^(0,2) - e^x
б) f(x) = ln(8 - 3x) + 8^x
f`(x) = (- 3)/(8 - 3x) + 8^x * ln8
2.
y = e^(4x - x²) [0;4]
Находим первую производную функции:
y' = (4 - 2x) * e^(4x - x²)
или
y' = 2*(2 - x) * e^(4x - x²)
Приравниваем ее к нулю:
(4 - 2x) * e^(4x - x²) = 0
e^(4x - x²) ≠ 0
4 - 2x = 0
x = 2
Вычисляем значения функции на концах отрезка
f(2) = e⁴
f(0) = 1
f(4) = 1
Ответ: fmin = 1, fmax = e⁴
1.
а) f(x) = x^(1,2) - e^x
f`(x) =1,2 * x^(1,2 - 1) - e^x = 1,2 * x^(0,2) - e^x
б) f(x) = ln(8 - 3x) + 8^x
f`(x) = (- 3)/(8 - 3x) + 8^x * ln8
2.
y = e^(4x - x²) [0;4]
Находим первую производную функции:
y' = (4 - 2x) * e^(4x - x²)
или
y' = 2*(2 - x) * e^(4x - x²)
Приравниваем ее к нулю:
(4 - 2x) * e^(4x - x²) = 0
e^(4x - x²) ≠ 0
4 - 2x = 0
x = 2
Вычисляем значения функции на концах отрезка
f(2) = e⁴
f(0) = 1
f(4) = 1
Ответ: fmin = 1, fmax = e⁴
Ответил mrsativaldyev
0
а можно ещё 1 номер пожалуйста?)
Ответил mrsativaldyev
0
для функции g (x)=e^-3x - 1/(3x+1) найдите первообразную, кот. в точке x0=0 принимала бы такое же значение, как и производная g (x) в этой точке.
Ответил mrsativaldyev
0
??
Новые вопросы
Русский язык,
2 года назад
Русский язык,
2 года назад
Алгебра,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад