335. Найдите корни уравнения: 2x² +9x-35 = 0; 2х-5 y²-81 (y + 2)²-49 (x+4)-(5x-1) 2x +1 б) B) = 0; = 0; г) e) (y²+4y+4)(2y-y-6) y-16 = 0; x-4x²+4x x²+3x-10 y-y²³-9y+9 y²-10y+21 = 0. = 0;
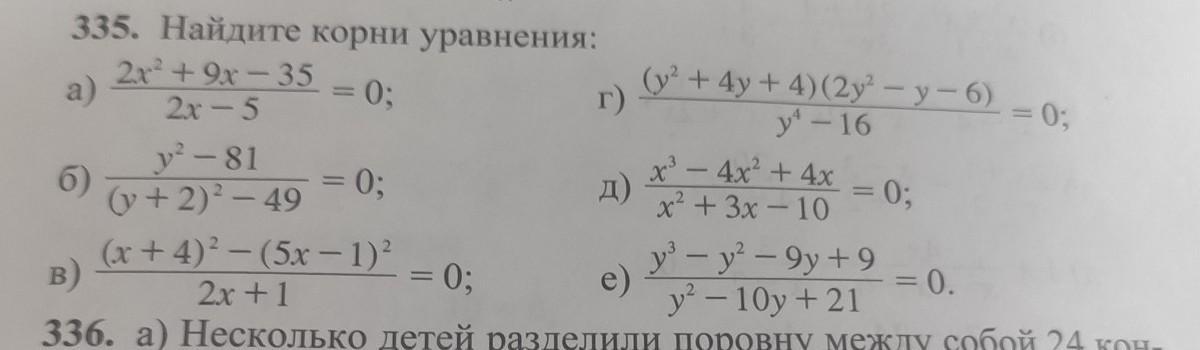
Ответы на вопрос
Ответ:
Давайте найдем корни уравнений:
а) \(\frac{2x^2 + 9x - 35}{2x - 5} = 0\)
Решение: \[2x^2 + 9x - 35 = 0\]
Факторизуем: \[(2x - 5)(x + 7) = 0\]
Отсюда получаем корни: \(x = \frac{5}{2}, -7\)
r) \[\frac{(y^2 + 4y + 4)(2y^2 - y - 6)}{y^4 - 16} = 0\]
Факторизуем числитель и знаменатель:
\[(y + 2)^2 \cdot (2y - 3)(y + 2)(y - 4)(y + 4) = 0\]
Отсюда получаем корни: \(y = -2, \frac{3}{2}, -4, 4\)
6) \[\frac{y^2 - 81}{(y + 2)^2 - 49} = 0\]
Факторизуем числитель и знаменатель:
\[(y - 9)(y + 9) \cdot ((y + 2) + 7)((y + 2) - 7) = 0\]
Отсюда получаем корни: \(y = -9, 9, -9, 5\)
B) \[\frac{(x + 4)^2 - (5x - 1)^2}{2x + 1} = 0\]
Решение: \[(x + 4 + 5x - 1)(x + 4 - 5x + 1) = 0\]
Отсюда получаем корни: \(x = -\frac{3}{4}, -\frac{5}{6}\)
д) \[\frac{x^3 - 4x^2 + 4x}{x^2 + 3x - 10} = 0\]
Решение: \[x(x - 2)(x - 2)(x + 5)(x - 1) = 0\]
Отсюда получаем корни: \(x = 0, 2, -5, 1\)
e) \[\frac{y^3 - y^2 - 9y + 9}{y^2 - 10y + 21} = 0\]
Решение: \[(y - 3)(y - 1)(y + 3)(y - 3)(y - 1) = 0\]
Отсюда получаем корни: \(y = 3, 1, -3\)
336. а) Несколько детей разделили поровну между собой 24 ко
(Продолжите вопрос, и я постараюсь вам помочь.)