Алгебра, вопрос задал veronikabelal630 , 1 год назад

27.2. Преобразуйте выражение в произведение: нужно только 2,4,6 пример, пожалуйста помогите, очень срочно нужно!!!60 баллов дам!​

Приложения:

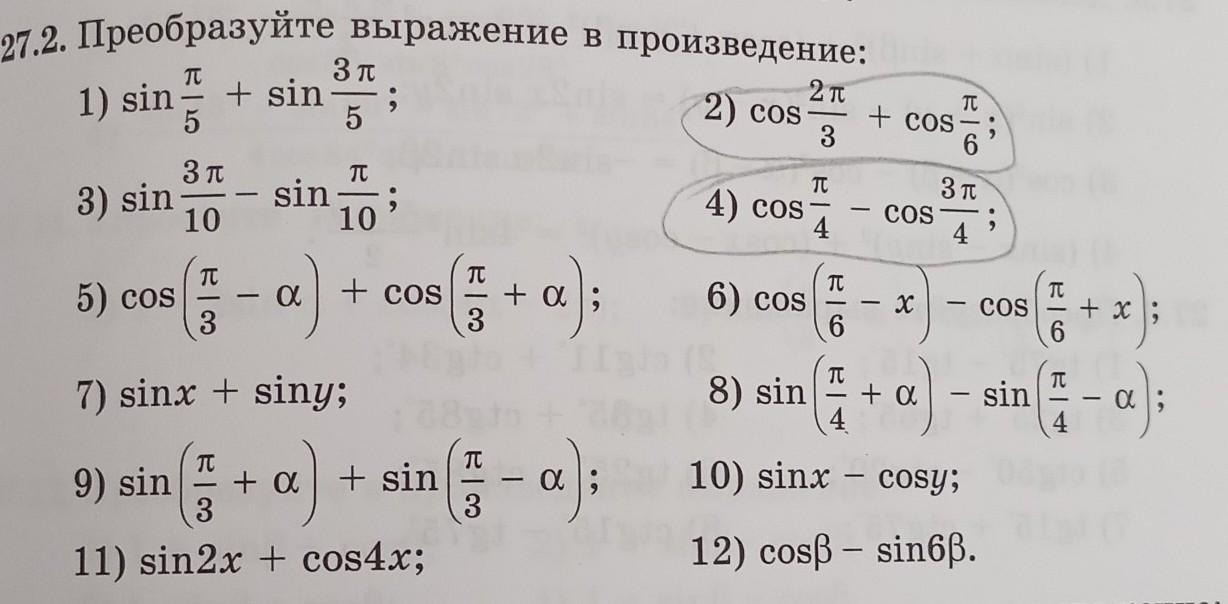
Ответы на вопрос

Ответил Universalka
3

\displaystyle\bf\\Cos\frac{2\pi }{3} +Cos\frac{\pi }{6} =2Cos\frac{\dfrac{2\pi }{3}+\dfrac{\pi }{6} }{2} \cdot Cos\frac{\dfrac{2\pi }{3}-\dfrac{\pi }{6} }{2} =\\\\\\=2Cos\frac{\dfrac{5\pi }{6} }{2}\cdot Cos\frac{\dfrac{3\pi }{6} }{2}=2Cos\frac{5\pi }{12} \cdot Cos\frac{3\pi }{12} =2Cos\frac{5\pi }{12} Cos\frac{\pi }{4} \\\\4)\\\\Cos\frac{\pi }{4} -Cos\frac{3\pi }{4} =-2Sin\frac{\dfrac{\pi }{4}+\dfrac{3\pi }{4} }{2} \cdot Sin\frac{\dfrac{\pi }{4}-\dfrac{3\pi }{4} }{2} =

\displaystyle\bf\\=-2Sin\frac{\pi }{2} \cdot Sin\Big(-\frac{\pi }{4} \Big)=2Sin\frac{\pi }{2} Sin\frac{\pi }{4} \\\\6)\\\\Cos\Big(\frac{\pi }{6}-x\Big)-Cos\Big(\frac{\pi }{6} +x\Big)=\\\\\\=-2Sin\frac{\dfrac{\pi }{6}-x+\dfrac{\pi }{6} +x }{2} \cdot Sin\frac{\dfrac{\pi }{6}-x-\dfrac{\pi }{6} -x }{2}=\\\\\\=-2Sin\frac{\dfrac{\pi }{3} }{2} \cdot Sin\frac{-2x}{2} =2Sin\frac{\pi }{6}\cdot Sinx

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Другие предметы, 1 год назад
Дайте відповідь на запитання на фото...
Українська мова, 1 год назад
Терміново‼️ Складіть речення за схемами:​...
Английский язык, 1 год назад
Ответьте пожалуйста на 2 задание True and Falsе и 4 задание.Пожалуйста дам 50 баллов‼️...
Русский язык, 1 год назад
Придумайте, пожалуйста, сказку, на абсолютно любую тему (уместную), где было бы много прилагательных в разных формах (только не перебарщивать). Примерно 18-20 предложений. (можно больше)...
Математика, 6 лет назад
X + 57 = 200 ПОМОГИТЕ! X + 57 - ( ) = 200...
Английский язык, 6 лет назад
помогите пожалуйста надо поставить слова по смыслу слова :choir ,stage orchestra,row, audience,exit,costume,​...