25 и 26, пожалуйста.
Приложения:

Ответы на вопрос
Ответил nafanya2014
0
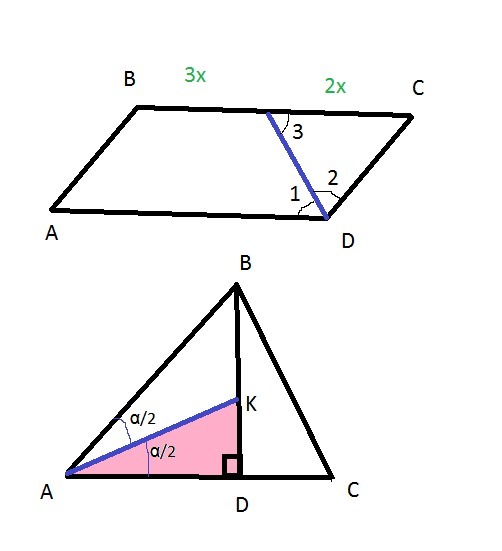
1) Пусть СЕ=2х, BE=3x
CE:BE=2x:3x=2:3
∠1=∠2 (биссектриса DE делит угол пополам)
∠1=∠3- внутренние накрест лежащие углы при ВС║AD и секущей DE.
Значит, ∠2=∠3
Δ DCE - равнобедренный
CE=CD=2x
AB=CD=2x - противоположные стороны параллелограмма равны
ВС=ВЕ+СЕ=3х+2х=5х
ВС=AD=5x
Р=2·(AB+BC)=2·(2x+5x)=14x=7·(2x)=7AB
2) Пусть ВК=13х, тогда KD=12x
BK:KD=13x:12x=13:12.
BD=BK+KD=13x+12x=25x
Биссектриса делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
Значит, BK:KD=AB:AD=13:12
AB=(13/12)AD
По теореме Пифагора из прямоугольного треугольника АВD:
AB²=BD²+AD²
(13/12)²AD²=(25x)²+AD² ⇒(25/144)AD²=625x²
AD=60x
Из прямоугольного треугольника АКD (∠KAD=α/2)
sin(α/2)=KD/AD=12x/60x=1/5
cos(α/2)=√(1-sin²(α/2))=√(1-(1/5)²)=(√24)/5
sin(∠A)=sinα=2sin(α/2)cos(α/2)=2·(1/5)·(√24)/5=(4√6)/25
По теореме синусов в Δ АВС:
ВС/sin(∠A)=2R
R=ВС/(2sin(∠A))=15/(2·(4√6)/25)=375/(8√6)=(125√6)/16
CE:BE=2x:3x=2:3
∠1=∠2 (биссектриса DE делит угол пополам)
∠1=∠3- внутренние накрест лежащие углы при ВС║AD и секущей DE.
Значит, ∠2=∠3
Δ DCE - равнобедренный
CE=CD=2x
AB=CD=2x - противоположные стороны параллелограмма равны
ВС=ВЕ+СЕ=3х+2х=5х
ВС=AD=5x
Р=2·(AB+BC)=2·(2x+5x)=14x=7·(2x)=7AB
2) Пусть ВК=13х, тогда KD=12x
BK:KD=13x:12x=13:12.
BD=BK+KD=13x+12x=25x
Биссектриса делит противоположную сторону на отрезки пропорциональные прилежащим сторонам.
Значит, BK:KD=AB:AD=13:12
AB=(13/12)AD
По теореме Пифагора из прямоугольного треугольника АВD:
AB²=BD²+AD²
(13/12)²AD²=(25x)²+AD² ⇒(25/144)AD²=625x²
AD=60x
Из прямоугольного треугольника АКD (∠KAD=α/2)
sin(α/2)=KD/AD=12x/60x=1/5
cos(α/2)=√(1-sin²(α/2))=√(1-(1/5)²)=(√24)/5
sin(∠A)=sinα=2sin(α/2)cos(α/2)=2·(1/5)·(√24)/5=(4√6)/25
По теореме синусов в Δ АВС:
ВС/sin(∠A)=2R
R=ВС/(2sin(∠A))=15/(2·(4√6)/25)=375/(8√6)=(125√6)/16
Приложения:
Новые вопросы
Математика,
2 года назад
История,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Литература,
9 лет назад
История,
9 лет назад