223.Вычислите.
224.Упростите выражение и найдите го значение
Тема: формулы сокращеного умножения. Помогите пожалуйста!!!!
Приложения:
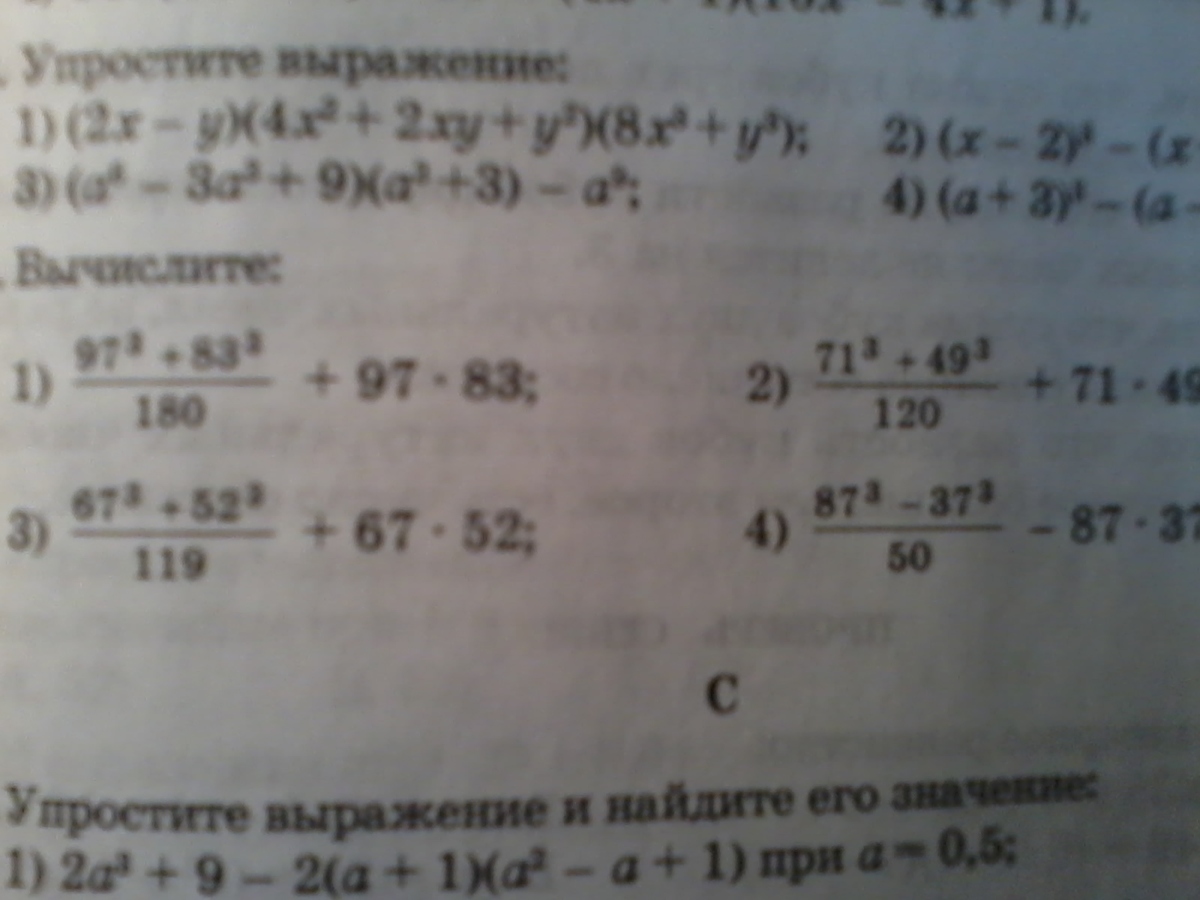
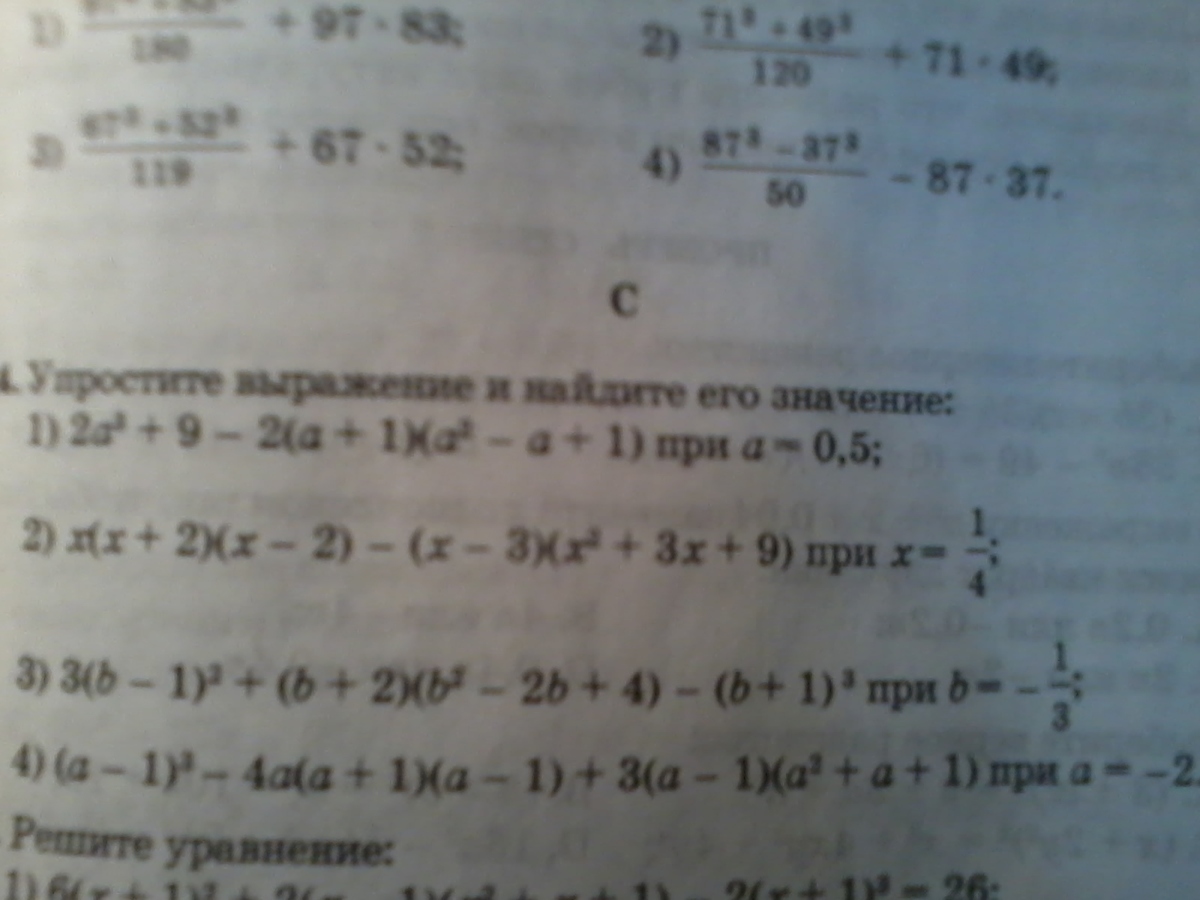
Ответы на вопрос
Ответил LopaAnt
0
223
1). ...= =
= 
2)...= =
= 
3)...= =
= 
4)...= =
= 
224
1). 2a^3 + 9 - 2(a+1)(a^2 - a + 1) = 2a^3 + 9 - 2(a^3 + 1) = 2a^3 + 9 - 2a^3 - 2 = 7
2). x(x+2)(x-2) - (x-3)(x^2+3x+9) = x(x^2 - 4) - (x^3 - 27) = x^3 - 4x - x^3 + 27 = -4x + 27 при х = 1/4: -4*1/4 + 27 = -1 + 27 = 26
3). 3(b-1)^3 + (b+2)(b^2-2b+4) - (b+1)^3 = 3(b^3 - 3b^2 + 3b - 1) + b^3 + 8 - (b^3 + 3b^2 + 3b + 1) = 3b^3 - 9b^2 + 9b - 3 + b^3 + 8 - b^3 - 3b^2 - 3b - 1 = 3b^3 - 12b^2 + 6b + 4
при b = -1/3
-3/27 - 12/9 - 6/3 + 4 = - 1/9 - 12/9 - 18/9 + 4 = -31/9 + 4 = (36-31)/9 = 5/9
4). (a-1)^3 - 4a(a+1)(a-1) + 3(a-1)(a^2+a+1) = a^3 - 3a^2 + 3a - 1 - 4a(a^2 - 1) + 3(a^3 - 1) = a^3 - 3a^2 + 3a - 1 - 4a^3 + 4 + 3a^3 - 3 = - 3a^2 + 3a
при а = -2
-3 * 4 + 3 * (-2) = -12 -6 = -18
1). ...=
2)...=
3)...=
4)...=
224
1). 2a^3 + 9 - 2(a+1)(a^2 - a + 1) = 2a^3 + 9 - 2(a^3 + 1) = 2a^3 + 9 - 2a^3 - 2 = 7
2). x(x+2)(x-2) - (x-3)(x^2+3x+9) = x(x^2 - 4) - (x^3 - 27) = x^3 - 4x - x^3 + 27 = -4x + 27 при х = 1/4: -4*1/4 + 27 = -1 + 27 = 26
3). 3(b-1)^3 + (b+2)(b^2-2b+4) - (b+1)^3 = 3(b^3 - 3b^2 + 3b - 1) + b^3 + 8 - (b^3 + 3b^2 + 3b + 1) = 3b^3 - 9b^2 + 9b - 3 + b^3 + 8 - b^3 - 3b^2 - 3b - 1 = 3b^3 - 12b^2 + 6b + 4
при b = -1/3
-3/27 - 12/9 - 6/3 + 4 = - 1/9 - 12/9 - 18/9 + 4 = -31/9 + 4 = (36-31)/9 = 5/9
4). (a-1)^3 - 4a(a+1)(a-1) + 3(a-1)(a^2+a+1) = a^3 - 3a^2 + 3a - 1 - 4a(a^2 - 1) + 3(a^3 - 1) = a^3 - 3a^2 + 3a - 1 - 4a^3 + 4 + 3a^3 - 3 = - 3a^2 + 3a
при а = -2
-3 * 4 + 3 * (-2) = -12 -6 = -18
Новые вопросы
Другие предметы,
2 года назад
Литература,
2 года назад
Физика,
9 лет назад
Алгебра,
9 лет назад
Геометрия,
9 лет назад