Алгебра, вопрос задал domtsvet56 , 6 лет назад

20 баллов. Упростить выражение.
((cos2b-cos6b)/(sin6b-sin2b))+tg2b

Приложения:

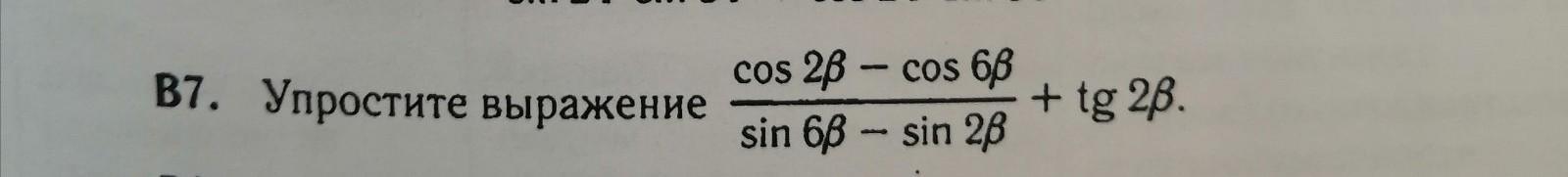
Ответы на вопрос

Ответил manyny06
3

Ответ:

решение смотри на фотографии

Приложения:
Ответил NNNLLL54
1

Ответ:

Формулы:   cosx-cosy=2sin\dfrac{x+y}{2}\cdot sin\dfrac{y-x}{2}   ,

                    sinx-siny=2sin\dfrac{x-y}{2}\cdot cos\dfrac{x+y}{2}  ,

                    sin(x+y)=sinx\cdot cosy+cosx\cdot siny  .

\dfrac{cos2\beta -cos6\beta }{sin6\beta -sin2\beta }+tg2\beta =\dfrac{2sin4\beta \cdot sin2\beta }{2sin2\beta \cdot cos4\beta }+\dfrac{sin2\beta }{cos2\beta }=\\\\\\=\dfrac{sin4\beta }{cos4\beta }+\dfrac{sin2\beta }{cos2\beta }=\dfrac{sin4\beta \cdot cos2\beta +cos4\beta \cdot sin2\beta }{cos4\beta \cdot cos2\beta }=\dfrac{sin6\beta }{cos4\beta \cdot cos2\beta }

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Английский язык, 1 год назад
Как пишется на английском слово кит...
Английский язык, 1 год назад
Помогите пожалуйста...
Биология, 6 лет назад
Помогите пожалуйста срочно! 6 класс Естествознание. ОТВЕТЫ С ДРУГИХ ВОПРОСОВ НЕ ПРИНИМАЮТСЯ! ⊂(・﹏・⊂)​...
Английский язык, 6 лет назад
language test 7A unit 7​...
Математика, 8 лет назад
а) -12 1/3 * 3 б) 4 1/4 * 2/3 в) -8 8/11 * (-4 1/8) г) 14/50 : (-14/25)...
Информатика, 8 лет назад
Дан массив чисел. Определить количество элементов, находящихся в интервале от1 до 12 и расположенных до максимального элемента массива. ПАСКАЛЬ.