2. Вероятность выпуска прибора, удовлетворяющего треброваниям качества, равна 0,9. В контрольной партии 3 прибора. Случайная величина X - число приборов, удовлетворяющих требованиям качества. а) найти закон распределения указанной случайной величины X и ее функцию распределения F(x).
b) вычислить математическое ожидание M(x), дисперсию D(x) и срелнее квадратическое отклонение Сигма(x)
Ответы на вопрос
Ответил maskkanal180
3
Ответ:
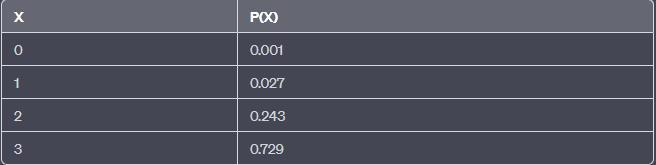
a) Случайная величина X - число приборов, удовлетворяющих требованиям качества. Вероятность того, что прибор удовлетворяет требованиям качества, равна 0,9. Вероятность того, что прибор не удовлетворяет требованиям качества, равна 0,1. Таким образом, распределение X - биномиальное, где n=3 и p=0,9.
Таблица распределения: картинка 1.png
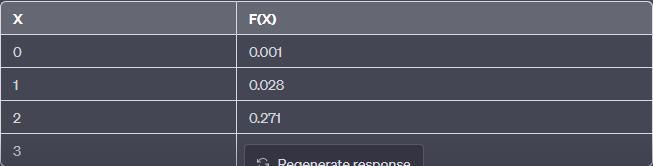
Функция распределения: картинка 2.png
b) Математическое ожидание (среднее значение) случайной величины X равно:
M(X) = np = 3 * 0,9 = 2,7
Дисперсия случайной величины X равна:
D(X) = np(1-p) = 3 * 0,9 * 0,1 = 0,27
Среднее квадратическое отклонение случайной величины X равно:
Сигма(X) = sqrt(D(X)) = sqrt(0,27) = 0,52
Пошаговое объяснение:
Приложения:
nikitosko32:
У чата GPT Спросил
Новые вопросы
ОБЖ,
11 месяцев назад
География,
11 месяцев назад
Математика,
1 год назад
Математика,
1 год назад
Химия,
6 лет назад