Алгебра, вопрос задал fima41987 , 6 лет назад

2)Упростите выражение :
$\frac{ \sin(\pi + \alpha ) \times \ctg(\pi - \alpha ) }{ \cos( \frac{\pi}{2} - \alpha ) }$

Приложения:

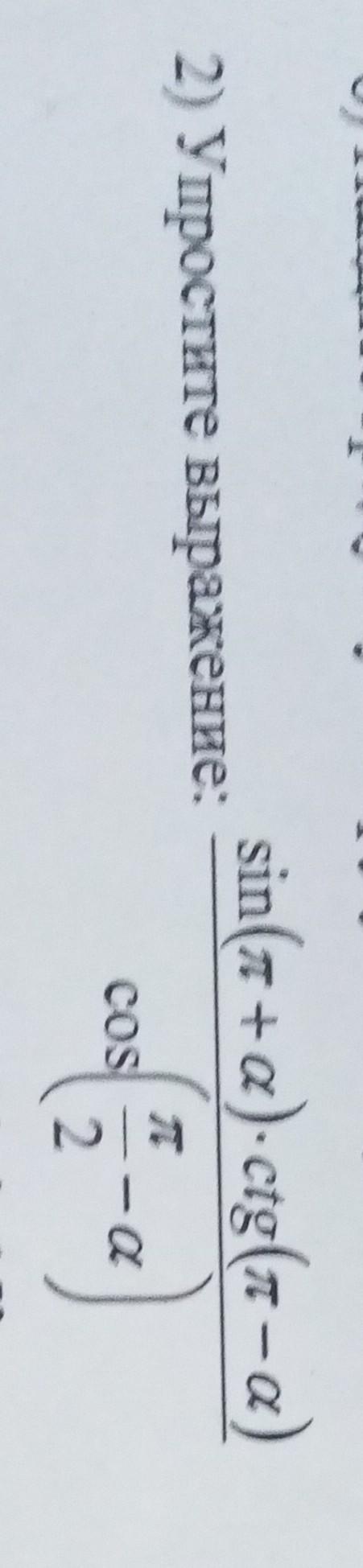
Ответы на вопрос

Ответил FaerVator

$\frac{ \sin(\pi + \alpha ) \cdot \cot(\pi - \alpha ) }{ \cos( \frac{\pi}{2} - \alpha ) } = \frac{ - \sin \alpha\cdot( - \cot \alpha ) }{ \sin \alpha } = - ( - \cot \alpha ) = \cot \alpha$

sin(π+α) заметим что sinπ это 180° , и плюс ещё альфа , значит это плюс ещё одна четверть т.е 180°+альфа это 3 четверть , теперь определимся знаками синус в 3 четверти отрицательный значит ставим минус как в решении.
cot(π-α) это 180° минус одна четверть то есть это 2 четверть . cot во 2-ой четверти отрицательный, значит ставим с минусом.
в знаменателе cos(π/2 -α) это половинчитое значение , значит соs меняем на sin
теперь сокращаем sinα и итого -(-соtα)=cotα

Приложения:

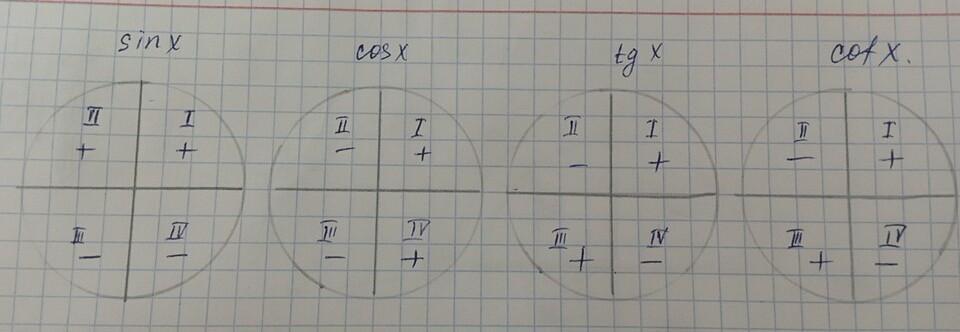
fima41987: от души

Jaguar444: хорош, одноклассник)

Ответил Jaguar444

Поясним:

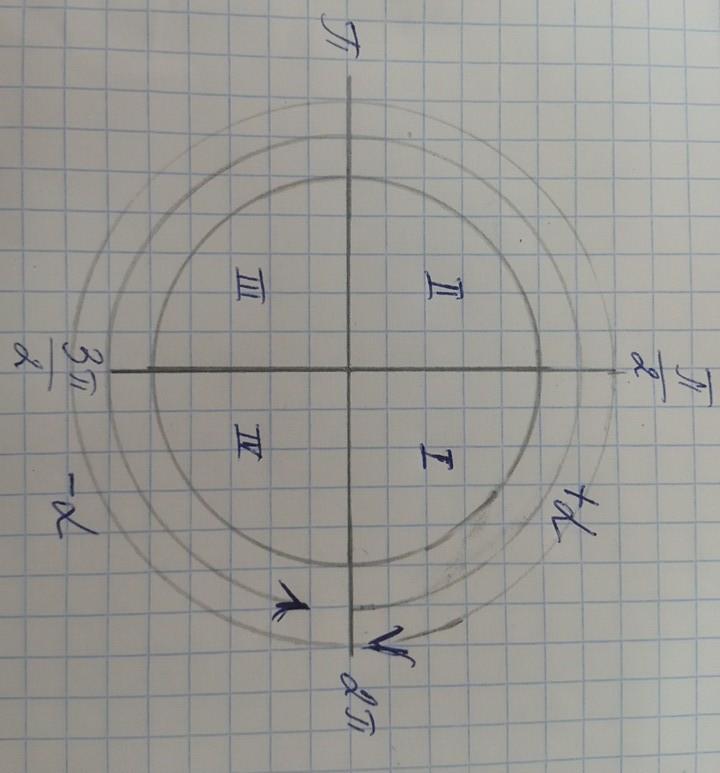
$\frac{ \sin(\pi + \alpha ) \times \cot(\pi - \alpha ) }{ \cos( \frac{\pi}{2} - \alpha ) } = \frac{ - \sin( \alpha ) \times ( - \cot \alpha )}{ \sin( \alpha ) } = - ( - \cot \alpha ) = \cot( \alpha )$

1) Мы обращаем внимание на знак "α", она положительная, π это 180°, он находится в третей четверти, а как нам известно, sin180° в третей четверти отрицательный.

2) в ctg π, "α" уже отрицательный, впереди ставим знак "-", -ctg π это второй четверть, а -ctg во второй четверти отрицательный.

Числитель разобрали, теперь переходим к знаменателю:

В cos π\2, "α" так же отрицательный, так же ставим знак "-", -cos π\2 находится в четвертой четверти, как нам известно, половинчатый угол меняет cos на sin) половинчатый угол как квадрат, знак "-" сокращает, и получается sin α.