Алгебра, вопрос задал danelbajturina12 , 6 лет назад

2 примера ответ дать с решением (алгебра 8 класс)
даю 60 баллов:)

Приложения:

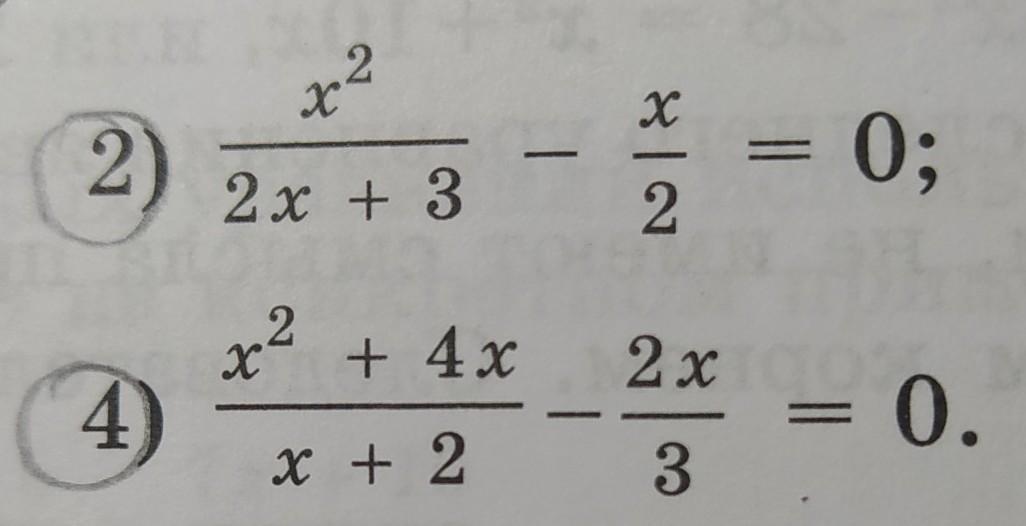
Ответы на вопрос

Ответил mathkot

1

Ответ:

1) $\boxed{x = 0}$

2) $\boxed{x_{1} = 0;x_{2} = -8}$

Объяснение:

2)

$\dfrac{x^{2} }{2x + 3} - \dfrac{x}{2} = 0$

ОДЗ: $2x + 3 \neq 0 \Longrightarrow x \neq -1,5$

$\dfrac{x^{2} }{2x + 3} = \dfrac{x}{2} \bigg | \cdot \dfrac{2}{2x + 3}$

$2x^{2} = x(2x + 3)$

$2x^{2} = 2x^{2} + 3x$

$3x = 0|:3$

$x = 0$

3)

$\dfrac{x^{2} + 4x}{x + 2} - \dfrac{2x}{3} = 0$

ОДЗ: $x + 2 \neq 0 \Longrightarrow x \neq-2$

$\dfrac{x^{2} + 4x}{x + 2} = \dfrac{2x}{3}$

$\dfrac{x^{2} + 4x}{x + 2} = \dfrac{2x}{3} \bigg | \cdot \dfrac{3}{x + 2}$

$3(x^{2} + 4x) = 2x(x + 2)$

$3x^{2} + 12x = 2x^{2} + 4x$

$x^{2} + 8x = 0$

$x(x + 8) = 0$

$x_{1} = 0;x_{2} = -8$

Ответил Universalka

1

$\displaystyle\bf\\2)\\\\\frac{x^{2} }{2x+3} -\frac{x}{2} =0\\\\\\\frac{2x^{2} -x\cdot(2x+3)}{2(2x+3)} =0\\\\\\\frac{2x^{2} -2x^{2} -3x}{2(2x+3)} =0\\\\\\-\frac{3x}{2(2x+3)} =0\\\\\\3x=0 \ \ ; \ \ 2x+3\neq 0\\\\\\x=0\\\\\\Otvet:0\\\\\\4)\\\\\frac{x^{2}+4x }{x+2} -\frac{2x}{3} =0\\\\\\\frac{3(x^{2} +4x)-2x\cdot(x+2)}{3(x+2)} =0\\\\\\\frac{3x^{2} +12x-2x^{2} -4x}{3(x+2)} =0\\\\\\\frac{x^{2} +8x}{3(x+2)} =0\\\\\\x^{2} +8x=0 \ \ ; \ \ x+2\neq 0\\\\\\x(x+8)=0$

$\displaystyle\bf\\x_{1}=0\\\\\\x+8=0\\\\\\x_{2} =-8\\\\\\Otvet:0 \ ; \ -8$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

как переводится слово техникой...

Русский язык, 1 год назад

семеро одного не ждут.синтактически разбор...

История, 6 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА ...

Қазақ тiлi, 6 лет назад

6-тапсырма. Төмендегі жағдаяттарды жалғастырып, шешімін табыңдар. Жауаптарыңды негіздеп, түсіндіріңдер. 1-жағдаят Сен аялдамада тұрсың. Адам көп. Автобус келіп тоқтады, адамдардың барлығы мінуге...

Геометрия, 8 лет назад

Помогите со вторым и третьим.

Биология, 8 лет назад

Ген курчавых волос доминирует над геном прямых волос; гетерозиготы имеют волнистые волосы. Ген, обуславливающий рыжий цвет волос, является рецессивным по отношению к гену темных волос. Гены,...