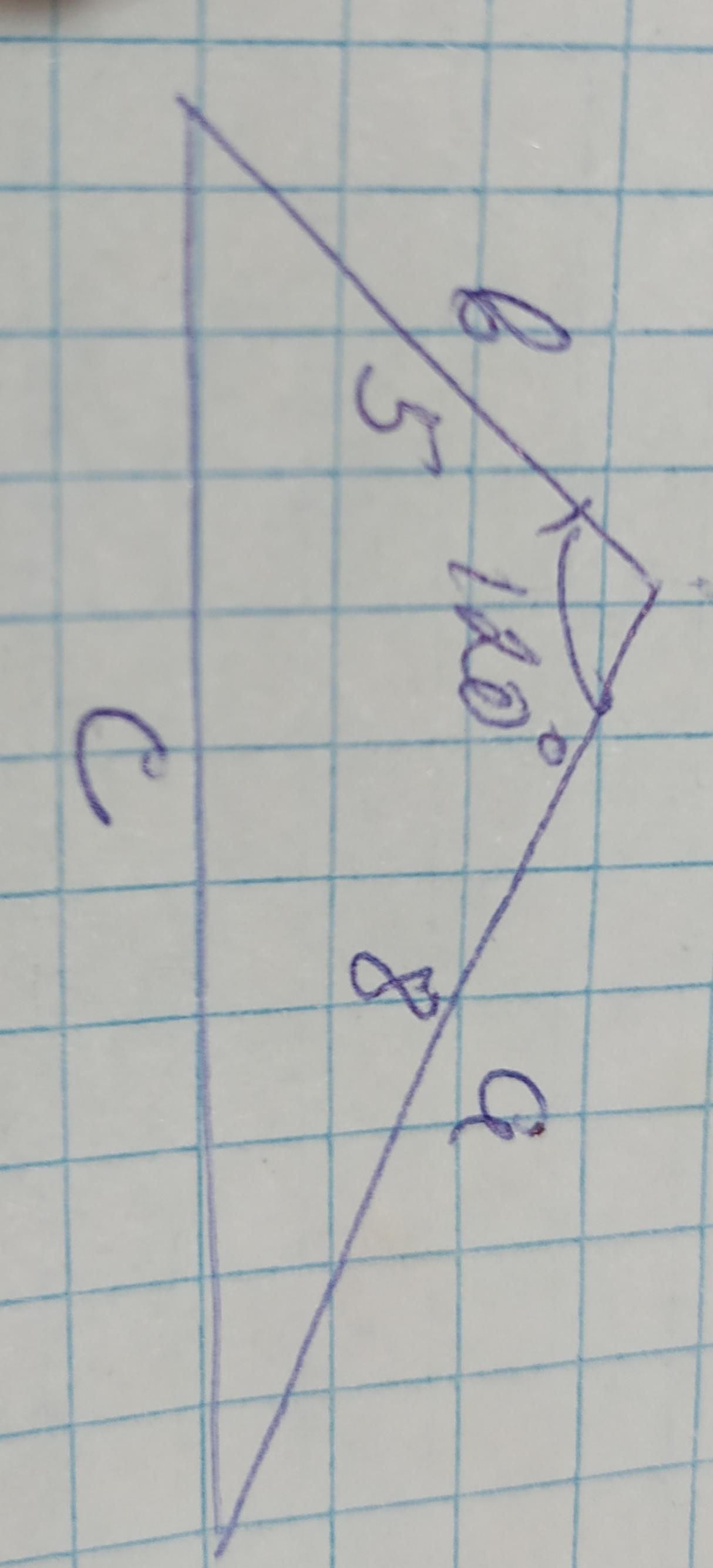
2. Нехай аib — сторони трикутника, ү — кут між ними. Знайдіть площу
трикутника, якщо a = 8 см, b = 5 см, 7 = 120°.
А. 103 см2. Б. 102 см. В. 10 см2. г. 20 см2.
​

Ответ: а) 10√3см²

Объяснение: найдём сторону с по теореме косинусов:

с²=а²+b²–2×ab×cos¥=8²+5²–2×8×5×(–1/2)=

=64+25+40=129; c=√129см

Далее зная все стороны треугольника найдём его площадь по формуле Герона:

S²=p(p–a)(p–b)(p–c), где р - полупериметр треугольника:

р=(а+b+c)/2=(8+5+√129)/2

Продолжение на фото