2.8. Решите уравнение: 1) 3x² - 4x=0; 5) y² -1/9=0 2) 4x²-9=0; 6) 6u2 - u = 0; 3) -5x²+6x=0; 7) 6m2-1=0; 4) -x²+3=0; 8) 2y +y²=0.
ПОМОГИТЕ ПАЖАЛУСТА
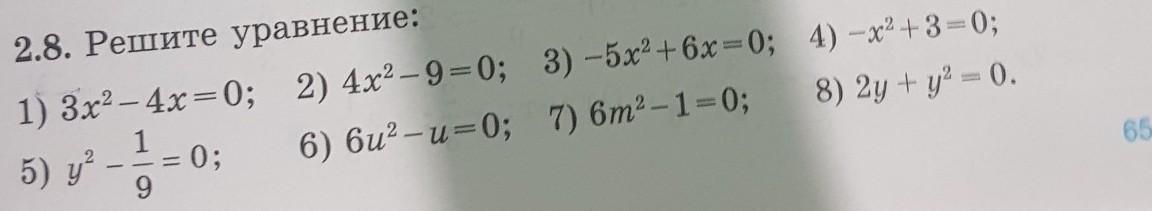
Ответы на вопрос
Ответ:
3x² – 4x = 0:
Сначала разложим на множители:
x(3x – 4) = 0
Теперь учтем, что здесь возможна ситуация, когда множитель равен нулю:
x = 0 или 3x – 4 = 0
Второе уравнение можно решить путем добавления 4 к обеим сторонам:
3x = 4
x = 4/3
Таким образом, решением уравнения является x=0 или x=4/3.
4x² – 9 = 0:
Разложим на множители:
(2x - 3)(2x + 3) = 0
Теперь учтем, что возможна ситуация, когда один из множителей равен нулю:
2x – 3 = 0 или 2x + 3 = 0
Решив эти два уравнения, имеем:
x = 3/2 или x = -3/2
Таким образом, решениями уравнения являются x=3/2 или x=-3/2.
-5x² + 6x = 0:
Разложим на множители:
x(-5x + 6) = 0
Учтем, что возможна ситуация, когда один из множителей равен нулю:
x = 0 или -5x + 6 = 0
Решив последнее уравнение, имеем:
x = 6/5
Таким образом, решениями уравнения являются x = 0 или x = 6/5.
-x² + 3 = 0:
Начнем с переноса всех терминов на одну сторону:
x² – 3 = 0
Разложим на множители справа:
(x - √3)(x + √3) = 0
Учтем, что возможна ситуация, когда один из множителей равен нулю:
x – √3 = 0 или x + √3 = 0
Решив эти два уравнения, имеем:
x = √3 или x = -√3
Таким образом, решениями уравнения являются x = √3 или x = -√3.
y² – 1/9 = 0:
Начнем с переноса 1/9 на другую сторону:
y² = 1/9
Далее учтем, что возможна ситуация, когда квадрат равен 1/9:
y = ±√(1/9)
y = ±1/3
Таким образом, решениями уравнения являются y = 1/3 или y = –1/3.
6u² – u = 0:
Разложим на множители:
u(6u – 1) = 0
Учтем, что возможна ситуация, когда один из множителей равен нулю:
u = 0 или 6u – 1 = 0
Решив последнее уравнение, имеем:
u = 1/6
Таким образом, решениями уравнения являются u=0 или u=1/6.
6m² – 1 = 0:
Начнём с переноса -1 на другую сторону:
6m² = 1
Разделим обе стороны на 6:
m² = 1/6
Решим квадратное уравнение путем взятия квадратного корня с обеих сторон:
m = ±√(1/6)
Таким образом, решениями уравнения являются m = √(1/6) или m = -√(1/6).
2y + y² = 0:
Разложим на множители:
y(2 + y) = 0
Учтем, что возможна ситуация, когда один из множителей равен нулю:
y = 0 или 2 + y = 0
Решив последнее уравнение, имеем:
y = -2
Таким образом, решениями уравнения являются y = 0 или y = –2.
Объяснение: