(2/13)^x-1 больше или равно 1
Приложения:
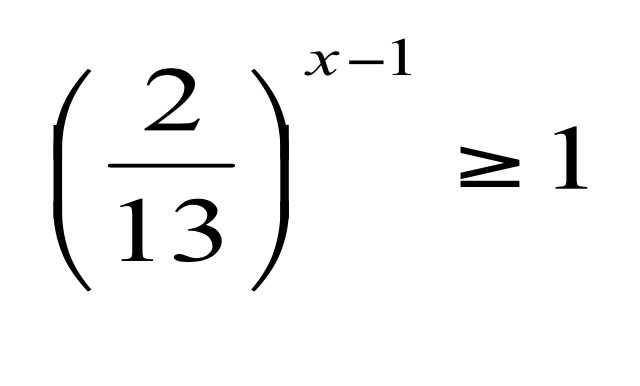
Ответы на вопрос
Ответил snoardekap4fn1c
0
(2/13)^(x - 1) ≥ 1;
(2/13)^(x - 1) ≥ (2/13)^0;
x - 1 ≤ 0;
x ≤ 1;
(2/13)^(x - 1) ≥ (2/13)^0;
x - 1 ≤ 0;
x ≤ 1;
Ответил snoardekap4fn1c
0
Поясню, что знак неравенство поменялся, так как a в функции a^x был меньше единицы и больше нуля.
Ответил matilda17562
0
Решение:
(2/13)^(x - 1) ≥ 1
(2/13)^(x - 1) ≥ (2/13)^0
у = (2/13)^х - убывающая функция, т.к. 0 < 2/13 < 1, тогда
х - 1 ≤ 0
х ≤ 1
х ∊ (- ∞ ; 1]
Ответ: (- ∞ ; 1]
(2/13)^(x - 1) ≥ 1
(2/13)^(x - 1) ≥ (2/13)^0
у = (2/13)^х - убывающая функция, т.к. 0 < 2/13 < 1, тогда
х - 1 ≤ 0
х ≤ 1
х ∊ (- ∞ ; 1]
Ответ: (- ∞ ; 1]
Новые вопросы
Физика,
1 год назад
Литература,
1 год назад
Геометрия,
7 лет назад
Алгебра,
7 лет назад
Математика,
8 лет назад